
 ��0����a-
��0����a-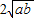 +b��0����a+b��2
+b��0����a+b��2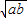 ��ֻ�е�a=bʱ���Ⱥų�����
��ֻ�е�a=bʱ���Ⱥų�����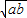 ��a��b��Ϊ��ʵ�����У���abΪ��ֵp����a+b��
��a��b��Ϊ��ʵ�����У���abΪ��ֵp����a+b��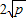 ��ֻ�е�a=bʱ��a+b����Сֵ2
��ֻ�е�a=bʱ��a+b����Сֵ2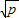 ��
��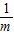 ����Сֵ______��
����Сֵ______��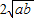 ����ָ���Ⱥų���ʱ��������
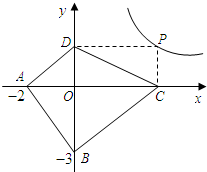
����ָ���Ⱥų���ʱ��������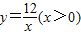 �ϵ�����һ�㣬����P��PC��x���ڵ�C��PO��y���ڵ�D�����ı���ABCD�������Сֵ����˵����ʱ�ı���ABCD����״��
�ϵ�����һ�㣬����P��PC��x���ڵ�C��PO��y���ڵ�D�����ı���ABCD�������Сֵ����˵����ʱ�ı���ABCD����״��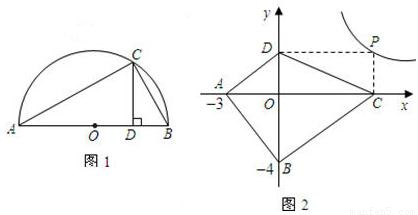
 ���۷֣�����СֵΪ2��
���۷֣�����СֵΪ2��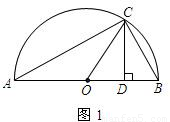
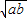 ��
��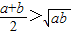 ��
�� ��
�� ����a+b��2
����a+b��2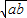 ����CD���ڰ뾶ʱ���Ⱥų�����
����CD���ڰ뾶ʱ���Ⱥų�����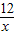 ����
����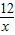 ����CA=x+3��DB=
����CA=x+3��DB=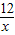 +4��
+4�� CA×DB=
CA×DB= ��x+3��×��
��x+3����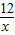 +4����
+4����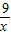 ��+12��
��+12��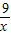 ��0��
��0��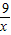 ��2
��2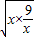 =6��
=6��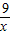 ����x=3ʱ���Ⱥų�����
����x=3ʱ���Ⱥų�����


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
| a |
| b |
| ab |
| ab |
| ab |
| p |
| p |
| 1 |
| m |
 �����˶��ٳ�ʱ����������F��С���Ƕ��٣�
�����˶��ٳ�ʱ����������F��С���Ƕ��٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| a |
| b |
| ab |
| ab |
| ab |
| p |
| p |
| 1 |
| m |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
 �Ķ����⣺����������ʵ��a��b��
�Ķ����⣺����������ʵ��a��b��| a |
| b |
| ab |
| ab |
| ab |
| p |
| p |
| 4 |
| x |
| 6 |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
| a |
| b |
| ab |
| ab |
| P |
| P |
| ab |

| 1 |
| m |
| 12 |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
 �Ķ����⣺
�Ķ����⣺| a |
| b |
| ab |
| ab |
| ab |
| p |
| p |
| 1 |
| m |
| 12 |
| x |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com