【题目】如图，已知点C是线段AB的中点，点D是线段AC的中点，点E是线段BC的中点．
（1）若线段DE=11cm，求线段AB的长．
（2）若线段CE=4cm，求线段DB的长．
科目：初中数学 来源： 题型：
【题目】如图，数轴上点A表示的数为8，B是数轴上一点，且AB＝14，动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t(t＞0)秒．
（1）点B表示的数为 ， 点P表示的数为（用含t的式子表示）；
（2）动点H从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P,H同时出发，问点P运动多少秒时追上点H?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】13世纪数学家斐波那契的（计算书）中有这样一个问题：“在罗马有7位老妇人，每人赶着7头毛驴，每头驴驮着7只口袋，每只口袋里装着7个面包，每个面包附有7把餐刀，每把餐刀有7只刀鞘”，则刀鞘数为（ ）
A.42
B.49
C.76
D.77
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 （2016柳州）如图1，抛物线
的顶点坐标为（0，﹣1），且经过点A（﹣2，0）．
（1）求抛物线的解析式；
（2）若将抛物线中在x轴下方的图象沿x轴翻折到x轴上方，x轴上方的图象保持不变，就得到了函数
图象上的任意一点，直线l是经过（0，1）且平行与x轴的直线，过点P作直线l的垂线，垂足为D，猜想并探究：PO与PD的差是否为定值？如果是，请求出此定值；如果不是，请说明理由．
（注：在解题过程中，如果你觉得有困难，可以阅读下面的材料）
附阅读材料：
1．在平面直角坐标系中，若A、B两点的坐标分别为A（
，
），B（
，
），则A，B两点间的距离为|AB|=
，这个公式叫两点间距离公式．
例如：已知A，B两点的坐标分别为（﹣1，2），（2，﹣2），则A，B两点间的距离为|AB|=
=5．
2．因式分解：
．
查看答案和解析>>
科目：初中数学 来源： 题型：
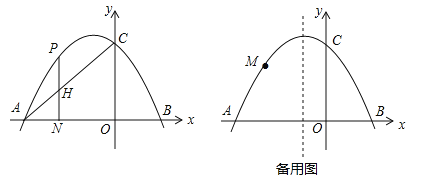
【题目】如图，在平面直角坐标系中，抛物线
交x轴于A，B两点，交y轴于点C（0，3），tan∠OAC=
．
（1）求抛物线的解析式；
（2）点H是线段AC上任意一点，过H作直线HN⊥x轴于点N，交抛物线于点P，求线段PH的最大值；
（3）点M是抛物线上任意一点，连接CM，以CM为边作正方形CMEF，是否存在点M使点E恰好落在对称轴上？若存在，请求出点M的坐标；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
