
【题目】如图,在正方形![]() 中,
中,![]() ,
,![]() 为
为![]() 上一动点,
上一动点,![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,下列有四个结论:①
,下列有四个结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 的周长为定值,其中正确的结论有( ).
的周长为定值,其中正确的结论有( ).

A.①②③B.①②④C.①③④D.①②③④
【答案】D
【解析】
①作辅助线,延长HF交AD于点L,连接CF,通过证明△ADF≌△CDF,可得:AF=CF,故需证明FC=FH,可证:AF=FH;②由FH⊥AE,AF=FH,可得:∠HAE=45°;③作辅助线,连接AC交BD于点O,证BD=2FG,只需证OA=GF即可,根据△AOF≌△FGH,可证OA=GF,故可证BD=2FG;④作辅助线,延长AD至点M,使AD=DM,过点C作CI∥HL,则IL=HC,可证AL=HE,再根据△MEC≌△MIC,可证:CE=IM,故△CEH的周长为边AM的长,为定值.
①连接FC,延长HF交AD于点L,

∵BD为正方形ABCD的对角线,
∴∠ADB=∠CDF=45°.
∵AD=CD,DF=DF,
∴△ADF≌△CDF.
∴FC=AF,∠ECF=∠DAF.
∵∠ALH+∠LAF=90°,
∴∠LHC+∠DAF=90°.
∵∠ECF=∠DAF,
∴∠FHC=∠FCH,
∴FH=FC.
∴FH=AF.
②∵FH⊥AE,FH=AF,
∴∠HAE=45°.
③连接AC交BD于点O,可知:BD=2OA,

∵∠AFO+∠GFH=∠GHF+∠GFH,
∴∠AFO=∠GHF.
∵AF=HF,∠AOF=∠FGH=90°,
∴△AOF≌△FGH.
∴OA=GF.
∵BD=2OA,
∴BD=2FG.
④连接EM,延长AD至点M,使AD=DM,过点C作CI∥HL,则:LI=HC,

∵HL⊥AE,CI∥HL,
∴AE⊥CI,
∴∠DIC+∠EAD=90°,∵∠EAD+∠AED=90°,
∴∠DIC=∠AED,
∵ED⊥AM,AD=DM,
∴EA=EM,
∴∠AED=∠MED,
∴∠DIC=∠DEM,
∴∠CIM=∠CEM,
∵CM=MC,∠ECM=∠CMI=45°,
∴△MEC≌△CIM,可得:CE=IM,
同理,可得:AL=HE,
∴HE+HC+EC=AL+LI+IM=AM=8.
∴△CEH的周长为8,为定值.
故①②③④结论都正确.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.

(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人沿相同的路线由![]() 到
到![]() 匀速行进,
匀速行进,![]() 两地间的路程为
两地间的路程为![]() 他们行进的路程
他们行进的路程![]() 与甲出发后的时间
与甲出发后的时间![]() 之间的函数图像如图所示.根据图像信息,下列说法正确的是( )
之间的函数图像如图所示.根据图像信息,下列说法正确的是( )

A.甲的速度是![]() B.乙的速度是
B.乙的速度是![]()
C.乙比甲晚出发![]() D.甲比乙晚到
D.甲比乙晚到![]() 地
地![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,将两张正方形纸片A与三张正方形纸片B放在一起(不重叠无缝隙),拼成一个宽为10的长方形,求正方形纸片A、B的边长.
(2)如图2,将一张正方形纸片D放在一正方形纸片C的内部,阴影部分的面积为4;如图3,将正方形纸片C、D各一张并列放置后构造一个新的正方形,阴影部分的面积为48,求正方形C、D的面积之和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在直线AB上,OC⊥OD,∠EDO与∠1互余.
(1)求证:ED//AB;
(2)OF平分∠COD交DE于点F,若∠OFD=65°,补全图形,并求∠1的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某城市接到台风警报,在该市正南方向![]() 的
的![]() 处有一台风中心,沿
处有一台风中心,沿![]() 方向以
方向以![]() 的速度移动,已知城市
的速度移动,已知城市![]() 到
到![]() 的距离
的距离![]() .
.
(1)台风中心经过多长时间从![]() 移动到
移动到![]() 点?
点?
(2)已知在距台风中心![]() 的圆形区域内都会受到不同程度的影响,若在点
的圆形区域内都会受到不同程度的影响,若在点![]() 的工作人员早上6:00接到台风警报,台风开始影响到台风结束影响要做预防工作,则他们要在什么时间段内做预防工作?
的工作人员早上6:00接到台风警报,台风开始影响到台风结束影响要做预防工作,则他们要在什么时间段内做预防工作?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售A,B两种品牌的多媒体教学设备,这两种多媒体教学设备的进价和售价如表所示.

(1)若该商场计划购进两种多媒体教学设备若干套,共需124万元,全部销售后可获毛利润36万元.则该商场计划购进A,B两种品牌的多媒体教学设备各多少套?
(2)通过市场调研,该商场决定在(1)中所购总数量不变的基础上,减少A种设备的购进数量,增加B种设备的购进数量.若用于购进这两种多媒体教学设备的总资金不超过120万元,且全部销售后可获毛利润不少于33.6万元.问有几种购买方案?并写出购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
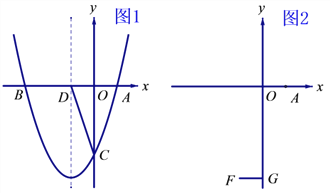
【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
, ![]() ,与
,与![]() 轴交于
轴交于![]() .
.
(1)若![]() ,求抛物线的解析式,并写出抛物线的对称轴;
,求抛物线的解析式,并写出抛物线的对称轴;
(2)如图1,在(1)的条件下,设抛物线的对称轴交轴于![]() ,在对称轴左侧的抛物线上有一点
,在对称轴左侧的抛物线上有一点![]() ,使
,使![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图2,设![]() ,
, ![]() 于
于![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() ?若存在,求
?若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com