
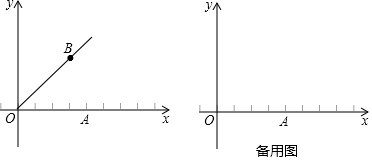
分析 (1)如图1中,作AF⊥OB于F,在OB上取一点E,使得∠AEF=30°,则d(A→OB)=AE.求出AE的长即可解决问题;
(2)如图2中,作GF⊥OB于F,∠GEO=30°,GE=2,推出FG=$\frac{1}{2}$EG=1,设直线x=1与直线OB交于点H,与x轴交于M,求出GM的值即可,同法可得G′的坐标;
(3)如图3中,作AF⊥直线l:y=kx+1于F,直线l交x轴于H,交y轴于G,设H(m,0),由△HOG∽△HFA,可得$\frac{OG}{AF}$=$\frac{HG}{AH}$,列出方程即可解决问题,同法可得当G在直线OB下方时G′(1,1-$\sqrt{2}$);
解答 解:(1)如图1中,作AF⊥OB于F,在OB上取一点E,使得∠AEF=30°,则d(A→OB)=AE.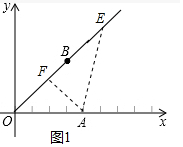
∵B(3,3),
∴∠AOF=∠OAF=45°,
∵OA=4,
∴AF=OF=2$\sqrt{2}$,
在Rt△AEF中,AE=2AF=4$\sqrt{2}$.
故答案为4$\sqrt{2}$.
(2)如图2中,作GF⊥OB于F,∠GEO=30°,GE=2,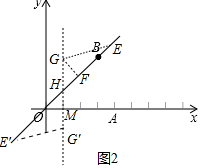
∴FG=$\frac{1}{2}$EG=1,
设直线x=1与直线OB交于点H,与x轴交于M,
∵∠GHF=∠HGF=45°,OM=HM=1,GF=HF=1,
∴GH=$\sqrt{2}$,
∴G(1,1+$\sqrt{2}$),
当G在直线OB下方时,同法可得G′(1,1-$\sqrt{2}$),
故答案为1+$\sqrt{2}$或1-$\sqrt{2}$.
(3)如图3中,作AF⊥直线l:y=kx+1于F,直线l交x轴于H,交y轴于G,设H(m,0),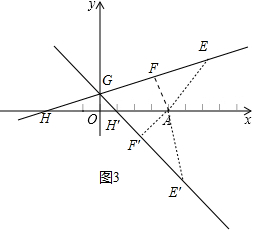
易知OG=1,AE=4,AF=2,OA=4,
由△HOG∽△HFA,
∴$\frac{OG}{AF}$=$\frac{HG}{AH}$,
∴$\frac{1}{2}$=$\frac{\sqrt{1+{m}^{2}}}{4-m}$
解得m=$\frac{-2\sqrt{13}-4}{3}$或$\frac{-2\sqrt{13}+4}{3}$(舍弃),
∴H($\frac{-2\sqrt{13}-4}{3}$,0),代入y=kx+1,得到k=$\frac{3}{2\sqrt{13}+4}$=$\frac{2\sqrt{13}-4}{12}$=$\frac{\sqrt{13}-2}{6}$,
当直线l经过一、二、四象限如图所示,同法可得k=-$\frac{3}{-4+2\sqrt{13}}$=-$\frac{\sqrt{13}+2}{6}$.
点评 本题考查一次函数综合题.直角三角形30度角性质、相似三角形的判定和性质、等腰三角形的性质和判定等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,正确寻找相似三角形解决问题,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
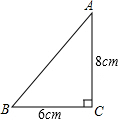 如图,一张三角形纸片ABC,∠C=90°,AC=8cm,BC=6cm.现将纸片折叠:使点A与点B重合,那么折痕长等于$\frac{15}{4}$cm.
如图,一张三角形纸片ABC,∠C=90°,AC=8cm,BC=6cm.现将纸片折叠:使点A与点B重合,那么折痕长等于$\frac{15}{4}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5.035×10-6 | B. | 50.35×10-5 | C. | 5.035×106 | D. | 5.035×10-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
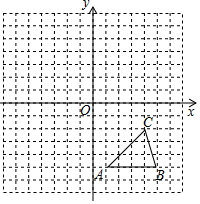 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-2).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:二次函数y=2x2+4x+m-1,与x轴的公共点为A,B.
已知:二次函数y=2x2+4x+m-1,与x轴的公共点为A,B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8251×102 | B. | 825.1×103 | C. | 82.51×104 | D. | 8.251×105 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com