
ЁОЬтФПЁПвЛИіВЛЭИУїДќзгжага![]() ИіКьЧђЃЌ
ИіКьЧђЃЌ![]() ИіТЬЧђКЭ
ИіТЬЧђКЭ![]() ИіАзЧђЃЌетаЉЧђГ§беЩЋЭтЮоЦфЫћВюБ№ЃЌ
ИіАзЧђЃЌетаЉЧђГ§беЩЋЭтЮоЦфЫћВюБ№ЃЌ
![]() ЕБ
ЕБ![]() ЪБЃЌДгДќжаЫцЛњУўГі
ЪБЃЌДгДќжаЫцЛњУўГі![]() ИіЧђЃЌУўЕНКьЧђКЭУўЕНАзЧђЕФПЩФмад (ЬюЁАЯрЭЌЁБЛђЁАВЛЯрЭЌЁБ)ЃЛ
ИіЧђЃЌУўЕНКьЧђКЭУўЕНАзЧђЕФПЩФмад (ЬюЁАЯрЭЌЁБЛђЁАВЛЯрЭЌЁБ)ЃЛ
![]() ДгДќжаЫцЛњУўГівЛИіЧђЃЌМЧТМЦфбеЩЋЃЌШЛКѓЗХЛиЃЌДѓСПжиИДИУЪЕбщЃЌЗЂЯжУўЕНТЬЧђЕФЦЕТЪЮШЖЈгк
ДгДќжаЫцЛњУўГівЛИіЧђЃЌМЧТМЦфбеЩЋЃЌШЛКѓЗХЛиЃЌДѓСПжиИДИУЪЕбщЃЌЗЂЯжУўЕНТЬЧђЕФЦЕТЪЮШЖЈгк![]() ЃЌдђ
ЃЌдђ![]() ЕФжЕЪЧ ЃЛ
ЕФжЕЪЧ ЃЛ
![]() дк
дк![]() ЕФЧщПіЯТЃЌШчЙћвЛДЮУўГіСНИіЧђЃЌЧыгУЪїзДЭМЛђСаБэЗЈЧѓУўГіЕФСНИіЧђбеЩЋВЛЭЌЕФИХТЪ.
ЕФЧщПіЯТЃЌШчЙћвЛДЮУўГіСНИіЧђЃЌЧыгУЪїзДЭМЛђСаБэЗЈЧѓУўГіЕФСНИіЧђбеЩЋВЛЭЌЕФИХТЪ.
ЁОД№АИЁПЃЈ1ЃЉЯрЭЌЃЛЃЈ2ЃЉ2ЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉШЗЖЈУўЕНКьЧђЕФИХТЪКЭУўЕНАзЧђЕФИХТЪЃЌБШНЯКѓМДПЩЕУЕНД№АИЃЛ
ЃЈ2ЃЉИљОнЦЕТЪМДПЩМЦЫуЕУГіnЕФжЕЃЛ
ЃЈ3ЃЉЛЪїзДЭММДПЩНтД№.
ЃЈ1ЃЉЕБn=1ЪБЃЌДќзгжаЙВ3ИіЧђЃЌ
ЁпУўЕНКьЧђЕФИХТЪЮЊ ![]() ЃЌУўЕНАзЧђЕФИХТЪЮЊ
ЃЌУўЕНАзЧђЕФИХТЪЮЊ![]() ЃЌ
ЃЌ
ЁпУўЕНКьЧђКЭУўЕНАзЧђЕФПЩФмадЯрЭЌЃЌ
ЙЪД№АИЮЊЃКЯрЭЌЃЛ
ЃЈ2ЃЉгЩЬтвтЕУЃК![]() ЃЌЕУn=2ЃЌ
ЃЌЕУn=2ЃЌ
ЙЪД№АИЮЊЃК2ЃЛ
ЃЈ3ЃЉЪїзДЭМШчЯТЃК

ИљОнЪїзДЭМГЪЯжЕФНсЙћПЩЕУЃК
![]() (УўГіЕФСНИіЧђбеЩЋВЛЭЌ)
(УўГіЕФСНИіЧђбеЩЋВЛЭЌ)![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
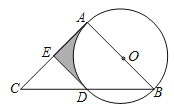
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌACЪЧЁбOЕФЧаЯпЃЌЧаЕуЮЊAЃЌBCНЛЁбOгкЕуDЃЌЕуEЪЧACЕФжаЕуЃЎ
ЃЈ1ЃЉЪдХаЖЯжБЯпDEгыЁбOЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєЁбOЕФАыОЖЮЊ2ЃЌЁЯBЃН50ЁуЃЌACЃН6ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
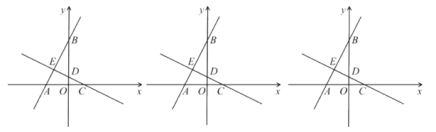
ЁОЬтФПЁПШчЙћЙигкxЕФВЛЕШЪНзщ жСЩйга3ИіећЪ§НтЃЌЧвЙигкxЕФЗжЪНЗНГЬ
жСЩйга3ИіећЪ§НтЃЌЧвЙигкxЕФЗжЪНЗНГЬ![]() ЕФНтЮЊећЪ§ЃЌдђЗћКЯЬѕМўЕФЫљгаећЪ§aЕФШЁжЕжЎКЭЮЊЃЈЁЁЁЁЃЉ
ЕФНтЮЊећЪ§ЃЌдђЗћКЯЬѕМўЕФЫљгаећЪ§aЕФШЁжЕжЎКЭЮЊЃЈЁЁЁЁЃЉ
A.Љ10B.Љ9C.Љ7D.Љ3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
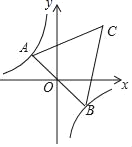
ЁОЬтФПЁПШчЭМЃЌдкЗДБШР§КЏЪ§yЃН-![]() ЕФЭМЯѓЩЯгавЛЖЏЕуAЃЌСЌНсAOВЂбгГЄНЛЭМЯѓЕФСэвЛжЇгкЕуBЃЌдкЕквЛЯѓЯоФкгавЛЕуCЃЌТњзуACЃНBCЃЌЕБЕуAдЫЖЏЪБЃЌЕуCЪМжедкКЏЪ§yЃН
ЕФЭМЯѓЩЯгавЛЖЏЕуAЃЌСЌНсAOВЂбгГЄНЛЭМЯѓЕФСэвЛжЇгкЕуBЃЌдкЕквЛЯѓЯоФкгавЛЕуCЃЌТњзуACЃНBCЃЌЕБЕуAдЫЖЏЪБЃЌЕуCЪМжедкКЏЪ§yЃН![]() ЕФЭМЯѓЩЯдЫЖЏЃЌШєtanЁЯCABЃН3ЃЌдђkЕФжЕЮЊЃЈЁЁЁЁЃЉ
ЕФЭМЯѓЩЯдЫЖЏЃЌШєtanЁЯCABЃН3ЃЌдђkЕФжЕЮЊЃЈЁЁЁЁЃЉ
A.![]() B.6C.8D.18
B.6C.8D.18
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌАыОЖЮЊ1ЕФ
жаЃЌАыОЖЮЊ1ЕФ![]() гы
гы![]() жсе§АыжсКЭ
жсе§АыжсКЭ![]() жсе§АыжсЗжБ№НЛгк
жсе§АыжсЗжБ№НЛгк![]() СНЕуЃЌжБЯп
СНЕуЃЌжБЯп![]() ЃК
ЃК![]() гы
гы![]() жсКЭ
жсКЭ![]() жсЗжБ№НЛгк
жсЗжБ№НЛгк![]() СНЕуЃЎ
СНЕуЃЎ
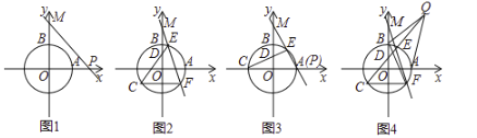
ЃЈlЃЉЕБжБЯп![]() гы
гы![]() ЯрЧаЪБЃЌЧѓГіЕу
ЯрЧаЪБЃЌЧѓГіЕу![]() ЕФзјБъКЭЕу
ЕФзјБъКЭЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЪБЃЌжБЯп
ЩЯЪБЃЌжБЯп![]() гы
гы![]() НЛгк
НЛгк![]() СНЕуЃЈЕу
СНЕуЃЈЕу![]() дкЕу
дкЕу![]() ЕФЩЯЗНЃЉЃЌЙ§Еу
ЕФЩЯЗНЃЉЃЌЙ§Еу![]() зї
зї![]() жсЃЌгы
жсЃЌгы![]() НЛгкСэвЛЕу
НЛгкСэвЛЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЎ
ЃЎ
ЂйШчЭМ3ЃЌШєЕу![]() гыЕу
гыЕу![]() жиКЯЪБЃЌЧѓ
жиКЯЪБЃЌЧѓ![]() ЕФГЄВЂаДГіНтД№Й§ГЬЃЛ
ЕФГЄВЂаДГіНтД№Й§ГЬЃЛ
ЂкШчЭМ2ЃЌШєЕу![]() гыЕу
гыЕу![]() ВЛжиКЯЪБЃЌ
ВЛжиКЯЪБЃЌ![]() ЕФГЄЪЧЗёЗЂЩњБфЛЏЃЌШєВЛЗЂЩњБфЛЏЃЌЧыЧѓГі
ЕФГЄЪЧЗёЗЂЩњБфЛЏЃЌШєВЛЗЂЩњБфЛЏЃЌЧыЧѓГі![]() ЕФГЄВЂаДГіНтД№Й§ГЬЃЛШєЗЂЩњБфЛЏЃЌЧыЫЕУїРэгЩЃЎ
ЕФГЄВЂаДГіНтД№Й§ГЬЃЛШєЗЂЩњБфЛЏЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШчЭМ4ЃЌдкЃЈ2ЃЉЕФЛљДЁЩЯЃЌСЌНс![]() ЃЌНЋЯпЖЮ
ЃЌНЋЯпЖЮ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЕН
ЕН![]() ЃЌШєЕу
ЃЌШєЕу![]() дк
дк![]() ЕФбгГЄЯпЪБЃЌЧыгУЕШЪНжБНгБэЪОЯпЖЮ
ЕФбгГЄЯпЪБЃЌЧыгУЕШЪНжБНгБэЪОЯпЖЮ![]() ЃЌ
ЃЌ![]() жЎМфЕФЪ§СПЙиЯЕЃЎ
жЎМфЕФЪ§СПЙиЯЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
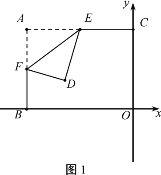
ЁОЬтФПЁПШчЭМ1ЃЌЦНУцжБНЧзјБъЯЕxoyжаЃЌA(Ѓ4ЃЌ3)ЃЌЗДБШР§КЏЪ§![]() ЕФЭМЯѓЗжБ№НЛОиаЮABOCЕФСНБпACЃЌBCгкEЃЌFЃЈEЃЌFВЛгыAжиКЯЃЉЃЌбизХEFНЋОиаЮABOCелЕўЪЙAЃЌDжиКЯЃЎ
ЕФЭМЯѓЗжБ№НЛОиаЮABOCЕФСНБпACЃЌBCгкEЃЌFЃЈEЃЌFВЛгыAжиКЯЃЉЃЌбизХEFНЋОиаЮABOCелЕўЪЙAЃЌDжиКЯЃЎ
 ЁЁЁЁЁЁЁЁЁЁ
ЁЁЁЁЁЁЁЁЁЁ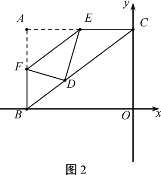
ЃЈ1ЃЉЂйШчЭМ2ЃЌЕБЕуDЧЁКУдкОиаЮABOCЕФЖдНЧЯпBCЩЯЪБЃЌЧѓCEЕФГЄЃЛ
ЂкШєелЕўКѓЕуDТфдкОиаЮABOCФкЃЈВЛАќРЈБпНчЃЉЃЌЧѓЯпЖЮCEГЄЖШЕФШЁжЕЗЖЮЇЃЎ
ЃЈ2ЃЉШєелЕўКѓЃЌЁїABDЪЧЕШбќШ§НЧаЮЃЌЧыжБНгаДГіДЫЪБЕуDЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕу![]() ЮЊзјБъдЕуЃЌ
ЮЊзјБъдЕуЃЌ![]() ЃЎжБЯп
ЃЎжБЯп![]() гы
гы![]() жсНЛгкЕуAЃЌНЛ
жсНЛгкЕуAЃЌНЛ![]() жсгкЕуBЃЎЙ§CЕузїжБЯпABЕФДЙЯпЃЌДЙзуЮЊEЃЌНЛ
жсгкЕуBЃЎЙ§CЕузїжБЯпABЕФДЙЯпЃЌДЙзуЮЊEЃЌНЛ![]() жсгкЕуDЃЎ
жсгкЕуDЃЎ
ЃЈ1ЃЉЧѓжБЯпCDЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуGЮЊ![]() жсИКАыжсЩЯвЛЕуЃЌСЌНгEGЃЌЙ§ЕуEзї
жсИКАыжсЩЯвЛЕуЃЌСЌНгEGЃЌЙ§ЕуEзї![]() НЛ
НЛ![]() жсгкЕуHЃЎЩшЕуGЕФзјБъЮЊ
жсгкЕуHЃЎЩшЕуGЕФзјБъЮЊ![]() ЃЌЯпЖЮAHЕФГЄЮЊ
ЃЌЯпЖЮAHЕФГЄЮЊ![]() ЃЎЧѓ
ЃЎЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЈВЛвЊЧѓаДГіздБфСПЕФШЁжЕЗЖЮЇЃЉ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЈВЛвЊЧѓаДГіздБфСПЕФШЁжЕЗЖЮЇЃЉ
ЃЈ3ЃЉЙ§ЕуCзї![]() жсЕФДЙЯпЃЌЙ§ЕуGзї
жсЕФДЙЯпЃЌЙ§ЕуGзї![]() жсЕФДЙЯпЃЌСНЯпНЛгкЕуMЃЌЙ§ЕуHзї
жсЕФДЙЯпЃЌСНЯпНЛгкЕуMЃЌЙ§ЕуHзї![]() гкЕуNЃЌНЛжБЯпCDгкЕу
гкЕуNЃЌНЛжБЯпCDгкЕу![]() ЃЌСЌНгMKЃЌШєMKЦНЗж
ЃЌСЌНгMKЃЌШєMKЦНЗж![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
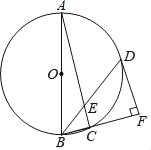
ЁОЬтФПЁПШчЭМЃЌЁїABCЪЧЁбOЕФФкНгдВЃЌЧвABЪЧЁбOЕФжБОЖЃЌЕуDдкЁбOЩЯЃЌBDЦНЗжЁЯABCНЛACгкЕуEЃЌDFЁЭBCНЛBCбгГЄЯпгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКDFЪЧЁбOЕФЧаЯпЃЎ
ЃЈ2ЃЉШє![]() ЃЌЧѓDEЕФГЄЃЎ
ЃЌЧѓDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛСаПьГЕДгМзЕидШЫйЪЛЭљввЕиЃЌвЛСаТ§ГЕДгввЕидШЫйЪЛЭљМзЕиЃЎЩшЯШЗЂГЕСОааЪЛЕФЪБМфЮЊxhЃЌСНГЕжЎМфЕФОрРыЮЊykmЃЌЭМжаЕФелЯпБэЪОyгыxжЎМфЕФКЏЪ§ЙиЯЕЃЌИљОнЭМЯѓНтОівдЯТЮЪЬтЃК
ЃЈ1ЃЉТ§ГЕЕФЫйЖШЮЊ_____km/hЃЌПьГЕЕФЫйЖШЮЊ_____km/hЃЛ
ЃЈ2ЃЉНтЪЭЭМжаЕуCЕФЪЕМЪвтвхВЂЧѓГіЕуCЕФзјБъЃЛ
ЃЈ3ЃЉЧѓЕБxЮЊЖрЩйЪБЃЌСНГЕжЎМфЕФОрРыЮЊ500kmЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com