
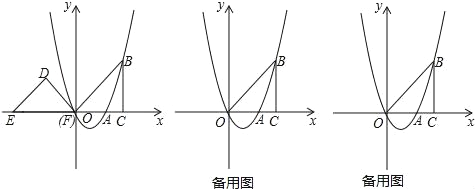
����Ŀ����ͼ��������y=ax2+bx��a��0��������A��2��0������B��3��3����BC��x���ڵ�C������OB������ֱ��������DEF��б��EF��x���ϣ���E������Ϊ��-4��0������F��ԭ���غ�
��1���������ߵĽ���ʽ��ֱ��д�����ĶԳ��
��2����DEF��ÿ��1����λ���ȵ��ٶ���x���������ƶ����˶�ʱ��Ϊt�룬����D����BC����ʱֹͣ�˶������DEF���OBC���ص����ֵ����ΪS�����S����t�ĺ�����ϵʽ��
��3����P�������߶Գ�����һ�㣬����ABP��ֱ��������ʱ����ֱ��д�����з��������ĵ�P���꣮
���𰸡���1��y=x2-2x���Գ�����ֱ��x=1����2���ٵ�0��t��3ʱ��S=![]() ���ڵ�3��t��4ʱ��S=
���ڵ�3��t��4ʱ��S=![]() ���۵�4��t��5ʱ��S=
���۵�4��t��5ʱ��S=![]() ����3����P����Ϊ��1��1������1��2������1��
����3����P������1��1������1��2������1��![]() ������1��
������1��![]() ����
����
��������
�����������1�����ݴ���ϵ�����������ʽ�ͶԳ��ἴ�ɣ�
��2����������������ٵ�0��t��3ʱ����DEF���OBC�ص�����Ϊ����ֱ�������Σ��ڵ�3��t��4ʱ����DEF���OBC�ص��������ı��Σ��۵�4��t��5ʱ����DEF���OBC�ص��������ı��εó�S����t�ĺ�����ϵʽ���ɣ�
��3��ֱ��д������ABP��ֱ��������ʱ���������ĵ�P���꣮
�����������1�����������![]() ��
��
���a=1��b=-2��
�������߽���ʽ��y=x2-2x��
�Գ�����ֱ��x=1��
��2����3�������
�ٵ�0��t��3ʱ����DEF���OBC�ص�����Ϊ����ֱ�������Σ���ͼ1��
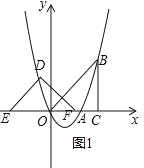
S=![]() ��
��
�ڵ�3��t��4ʱ����DEF���OBC�ص��������ı��Σ���ͼ2��
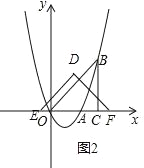
S=![]() ��
��
�۵�4��t��5ʱ����DEF���OBC�ص��������ı��Σ���ͼ3��
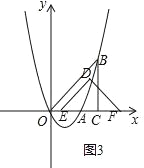
S=![]() ��
��
��3������ABP��ֱ��������ʱ���ɵ÷��������ĵ�P����Ϊ��1��1������1��2������1��![]() ������1��
������1��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ρ����Ρ������ζ����е������ǣ� ��
A. �Խ�������һ���ƽ�� B. �Խ�������һ��ഹֱƽ��
C. �Խ�����ƽ�� D. ��������ȣ��ĸ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ� ��
A.��2��a+b��=��2a+2b
B.x5+x5=x
C.a6��a4=a2
D.3a22a3=6a5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�������Ƿ���x2+2006x+1=0������������1+2008��+��2����1+2008��+��2����ֵΪ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���GΪ��ABC�����ģ�����CG���ӳ���AB�ڵ�D����֪GD=2����CD=____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������OABC�У�AB��OC����A����Ϊ��0��6������C����Ϊ��3��0����BC=![]() ��һ�����߹���A��B��C��
��һ�����߹���A��B��C��
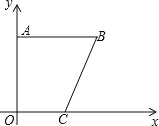
��1����գ���B������Ϊ ��
��2����������ߵĽ���ʽ��
��3����ƽ����x���ֱ����x���Ϸ��������߽��ڵ�E��F����EFΪֱ����Բǡ����x�����У����Բ�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������κ���y=x2��ͼ������ƽ��1����λ����ƽ�ƺ�Ķ��κ����Ľ���ʽΪ�� ��
A. y= (x��1)2 B. y=(x+1)2 C. y= x2 ��1 D. y= x2 +1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��֯�������ʵ�����Ϊ300��ѧ��ÿ�˷���һƿ��Ȫˮ�����˷��������أ�Ϊ�˸�У����С��Կ�Ȫˮ���˷�������г������飬����������Ȫˮ�ȵ��������ͳ�ƣ����¿ɷ�Ϊ���֣�
A��ȫ�����ꣻ
B����ʣԼ![]() ��
��
C����ʣԼһ�룻
D����ƿ������δ�ȣ�
ͬѧ�Ǹ���ͳ�ƽ�����Ƴ��������Ų�������ͳ��ͼ������ͳ��ͼ�ṩ����Ϣ������������⣺
��1�����ε����� ��ѧ������ͼ��2����D�������ε�Բ�Ľ��� �ȣ�
��2���벹ȫ����ͳ��ͼ��
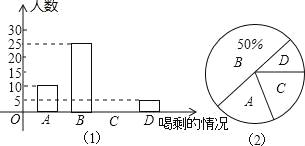
��3�������������ʵ������˷ѵĿ�Ȫˮ����ƿ������δ����ȫ���˷ѣ�500ml�ۺ�Ϊһƿ��Լ�ж���ƿ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʱ��2016��2��11��23��30�֣���ѧ�������������״�ֱ��̽�����������ӡ֤�˰���˹̹100��ǰ��Ԥ�ԣ�������̽����LIGO����Ҫ�������������ഹֱ�ij��ۣ�ÿ���۳�4000�ף�����4000�ÿ�ѧ��������ʾΪ��������
A. 0.4��103 B. 0.4��104 C. 4��103 D. 4��104
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com