
ЁОЬтФПЁПСНИіШ§НЧАх![]() ЃЌ
ЃЌ![]() ЃЌАДШчЭМЫљЪОЕФЮЛжУАкЗХЃЌЕу
ЃЌАДШчЭМЫљЪОЕФЮЛжУАкЗХЃЌЕу![]() гыЕу
гыЕу![]() жиКЯЃЌБп
жиКЯЃЌБп![]() гыБп
гыБп![]() дкЭЌвЛЬѕжБЯпЩЯЃЈМйЩшЭМаЮжаЫљгаЕФЕуЃЌЯпЖМдкЭЌвЛЦНУцФкЃЉЃЎЦфжаЃЌ
дкЭЌвЛЬѕжБЯпЩЯЃЈМйЩшЭМаЮжаЫљгаЕФЕуЃЌЯпЖМдкЭЌвЛЦНУцФкЃЉЃЎЦфжаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎЯжЙЬЖЈШ§НЧАх
ЃЎЯжЙЬЖЈШ§НЧАх![]() ЃЌНЋШ§НЧАх
ЃЌНЋШ§НЧАх![]() биЩфЯп
биЩфЯп![]() ЗНЯђЦНвЦЃЌЕБЕу
ЗНЯђЦНвЦЃЌЕБЕу![]() ТфдкБп
ТфдкБп![]() ЩЯЪБЭЃжЙдЫЖЏЃЎЩшШ§НЧАхЦНвЦЕФОрРыЮЊ
ЩЯЪБЭЃжЙдЫЖЏЃЎЩшШ§НЧАхЦНвЦЕФОрРыЮЊ![]() ЃЌСНИіШ§НЧАхжиЕўВПЗжЕФУцЛ§ЮЊ
ЃЌСНИіШ§НЧАхжиЕўВПЗжЕФУцЛ§ЮЊ![]() ЃЎ
ЃЎ

ЃЈ1ЃЉЕБЕу![]() ТфдкБп
ТфдкБп![]() ЩЯЪБЃЌ
ЩЯЪБЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§НтЮіЪНЃЌВЂаДГіздБфСП
ЕФКЏЪ§НтЮіЪНЃЌВЂаДГіздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЩшБп![]() ЕФжаЕуЮЊЕу
ЕФжаЕуЮЊЕу![]() ЃЌБп
ЃЌБп![]() ЕФжаЕуЮЊЕу
ЕФжаЕуЮЊЕу![]() ЃЎжБНгаДГідкШ§НЧАхЦНвЦЙ§ГЬжаЃЌЕу
ЃЎжБНгаДГідкШ§НЧАхЦНвЦЙ§ГЬжаЃЌЕу![]() гыЕу
гыЕу![]() жЎМфОрРыЕФзюаЁжЕЃЎ
жЎМфОрРыЕФзюаЁжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ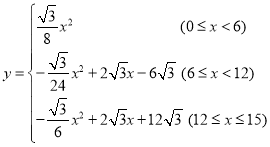 ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃК
ЃЈ1ЃЉгЩШёНЧШ§НЧКЏЪ§ЃЌЕУЕН![]() ЕФГЄЃЌНјЖјПЩЕУ
ЕФГЄЃЌНјЖјПЩЕУ![]() ЕФГЄЃЌгЩОиаЮЕФаджЪЃЌПЩЕУД№АИЃЛ
ЕФГЄЃЌгЩОиаЮЕФаджЪЃЌПЩЕУД№АИЃЛ
ЃЈ2ЃЉЗжРрЬжТлЃКЂйЕБ![]() ЪБЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНЃЌПЩЕУД№АИЃЛЂкЕБ
ЪБЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНЃЌПЩЕУД№АИЃЛЂкЕБ![]() ЪБЃЌ
ЪБЃЌ
ЂлЕБ![]() ЪБЃЌИљОнУцЛ§ЕФКЭВюЃЌПЩЕУД№АИЃЛ
ЪБЃЌИљОнУцЛ§ЕФКЭВюЃЌПЩЕУД№АИЃЛ
ЃЈ3ЃЉИљОнЕугыжБЯпЩЯЫљгаЕуЕФСЌЯпжаДЙЯпЖЮзюЖЬЃЌПЩЕУ![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЌИљОнШ§НЧаЮЕФ
ЩЯЃЌИљОнШ§НЧаЮЕФ
жаЮЛЯпЃЌПЩЕУ![]() ЕФГЄЃЌИљОнШёНЧШ§НЧКЏЪ§ЃЌПЩЕУ
ЕФГЄЃЌИљОнШёНЧШ§НЧКЏЪ§ЃЌПЩЕУ![]() ЕФГЄЃЌИљОнЯпЖЮЕФКЭВюЃЌПЩЕУД№АИЃЎ
ЕФГЄЃЌИљОнЯпЖЮЕФКЭВюЃЌПЩЕУД№АИЃЎ
ЪдЬтНтЮіЃК
НтЃКЃЈ1ЃЉШчЭМ1ЫљЪОЃКзї![]() гк
гк![]() ЕуЃЎ
ЕуЃЎ
дк![]() жаЃЌгЩ
жаЃЌгЩ![]() ЃЌ
ЃЌ![]() ЃЌЕУЃК
ЃЌЕУЃК![]() =
=![]() ЃЎ
ЃЎ
дк![]() жаЃЌ
жаЃЌ![]() ЃЎЫФБпаЮ
ЃЎЫФБпаЮ![]() ЪЧОиаЮЃЌ
ЪЧОиаЮЃЌ![]() ЃЌЙЪД№АИЮЊЃК
ЃЌЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ
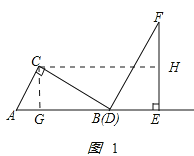
ЃЈ2ЃЉЂйЕБ![]() ЪБЃЌШчЭМ2ЫљЪОЃЎ
ЪБЃЌШчЭМ2ЫљЪОЃЎ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕУЃК
ЃЌЕУЃК![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
жиЕўВПЗжЕФУцЛ§ЮЊ![]() ЃЛ
ЃЛ
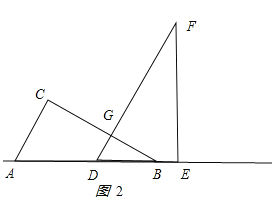
ЂкЕБ![]() ЪБЃЌШчЭМ3ЫљЪОЃЎ
ЪБЃЌШчЭМ3ЫљЪОЃЎ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
жиЕўВПЗжЕФУцЛ§ЮЊ![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
ЛЏМђЃЌЕУ![]() ЃЛ
ЃЛ
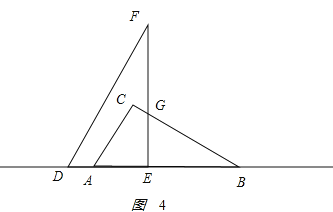
ЂлЕБ![]() ЪБЃЌШчЭМ4ЫљЪОЃЎ
ЪБЃЌШчЭМ4ЫљЪОЃЎ
![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
жиЕўВПЗжЕФУцЛ§ЮЊ![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
ЛЏМђЃЌЕУ![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃК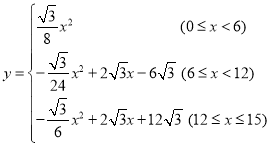 ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ5ЫљЪОзї![]() гк
гк![]() ЕуЃЎ
ЕуЃЎ
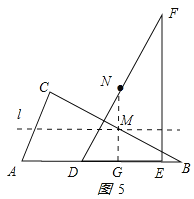
Еу![]() дк
дк![]() ЩЯЪБ
ЩЯЪБ![]() зюЖЬЃЌ
зюЖЬЃЌ![]() ЪЧ
ЪЧ![]() ,
,![]() ЃЎ
ЃЎ ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()


 КУГЩМЈ1Мг1ЦкФЉГхДЬ100ЗжЯЕСаД№АИ
КУГЩМЈ1Мг1ЦкФЉГхДЬ100ЗжЯЕСаД№АИ Н№зДдЊМЈгХКУОэЯЕСаД№АИ
Н№зДдЊМЈгХКУОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПРћгУЗДжЄЗЈжЄУїУќЬтЁАЫФБпаЮжажСЩйгавЛИіНЧЪЧЖлНЧЛђжБНЧЁБЪБЃЌгІМйЩш( )
A. ЫФБпаЮжажСЖргавЛИіФкНЧЪЧЖлНЧЛђжБНЧ
B. ЫФБпаЮжаЫљгаФкНЧЖМЪЧШёНЧ
C. ЫФБпаЮЕФУПвЛИіФкНЧЖМЪЧЖлНЧЛђжБНЧ
D. ЫФБпаЮжаЫљгаФкНЧЖМЪЧжБНЧ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
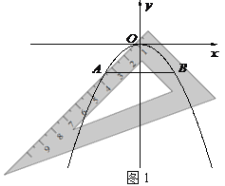
ЁОЬтФПЁПЪ§жсЩЯЕуAЁЂBжЎМфЕФОрРыЮЊ5ЃЌдђЫќУЧБэЪОЕФЪ§ПЩФмЪЧ
A. Ѓ2ЃЌ3 B. 3ЃЌ2 C. Ѓ2ЃЌ7 D. Ѓ3ЃЌЃ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋжБЯпy=2x-5ЯђЩЯЦНвЦ2ИіЕЅЮЛЃЌЫљЕУжБЯпНтЮіЪНЮЊ__________ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁППзУїЪЧвЛИіЯВЛЖЬНОПзъбаЕФЭЌбЇЃЌЫћдкКЭЭЌбЇУЧвЛЦ№баОПФГЬѕХзЮяЯп![]() ЕФаджЪЪБЃЌНЋвЛАбжБНЧШ§НЧАхЕФжБНЧЖЅЕужУгкЦНУцжБНЧзјБъЯЕЕФдЕу
ЕФаджЪЪБЃЌНЋвЛАбжБНЧШ§НЧАхЕФжБНЧЖЅЕужУгкЦНУцжБНЧзјБъЯЕЕФдЕу![]() ЃЌСНжБНЧБпгыИУХзЮяЯпНЛгк
ЃЌСНжБНЧБпгыИУХзЮяЯпНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЧыНтД№вдЯТЮЪЬтЃК
СНЕуЃЌЧыНтД№вдЯТЮЪЬтЃК
ЃЈ1ЃЉШєВтЕУ![]() ЃЈШчЭМ1ЃЉЃЌЧѓ
ЃЈШчЭМ1ЃЉЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЖдЭЌвЛЬѕХзЮяЯпЃЌПзУїНЋШ§НЧАхШЦЕу![]() а§зЊЕНШчЭМ2ЫљЪОЮЛжУЪБЃЌЙ§
а§зЊЕНШчЭМ2ЫљЪОЮЛжУЪБЃЌЙ§![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌВтЕУ
ЃЌВтЕУ![]() ЃЌаДГіДЫЪБЕу
ЃЌаДГіДЫЪБЕу![]() ЕФзјБъЃЌВЂЧѓЕу
ЕФзјБъЃЌВЂЧѓЕу![]() ЕФКсзјБъЃЛ
ЕФКсзјБъЃЛ
ЃЈ3ЃЉЖдИУХзЮяЯпЃЌПзУїНЋШ§НЧАхШЦЕу![]() а§зЊШЮвтНЧЖШЪБОЊЦцЕиЗЂЯжЃЌНЛЕу
а§зЊШЮвтНЧЖШЪБОЊЦцЕиЗЂЯжЃЌНЛЕу![]() ЁЂ
ЁЂ![]() ЕФСЌЯпЖЮзмОЙ§вЛИіЙЬЖЈЕФЕуЃЌЪдЫЕУїРэгЩВЂЧѓГіИУЕуЕФзјБъЃЎ
ЕФСЌЯпЖЮзмОЙ§вЛИіЙЬЖЈЕФЕуЃЌЪдЫЕУїРэгЩВЂЧѓГіИУЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУРжмФЉРДЕНЙЋдАЃЌЗЂЯждкЙЋдАвЛНЧгавЛжжЁАЪижъД§ЭУЁБгЮЯЗЁЃгЮЯЗЩшМЦепЬсЙЉСЫвЛжЛЭУзгКЭвЛИігаAЁЂBЁЂCЁЂDЁЂEЮхИіГіШыПкЕФЭУС§ЃЌЖјЧвС§ФкЕФЭУзгДгУПИіГіШыПкзпГіЭУС§ЕФЛњЛсЪЧОљЕШЕФЁЃЙцЖЈЃКЂйЭцМвжЛФмНЋаЁЭУДгAЁЂBСНИіГіШыПкЗХШыЃЛ
ЂкШчЙћаЁЭУНјШыС§згКѓбЁдёДгПЊЪМНјШыЕФГіШыПкРыПЊЃЌдђПЩЛёЕУвЛжЛМлжЕ5дЊаЁЭУЭцОпЃЌЗёдђгІИЖЗб3дЊЁЃ
ЃЈ1ЃЉЁЂЮЪаЁУРЕУЕНаЁЭУЭцОпЕФЛњЛсгаЖрДѓЃП
ЃЈ2ЃЉЁЂМйЩшга100ШЫДЮЭцДЫгЮЯЗЃЌЙРМЦгЮЯЗЩшМЦепПЩзЌЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаДГівЛИіжсЖдГЦЭМаЮЕЋВЛЪЧжааФЖдГЦЭМаЮЕФЫФБпаЮЃК__________________
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
A.ШєaЁЂbЁЂcЪЧЁїABCЕФШ§БпЃЌдђa2b2c2ЃЛ
B.ШєaЁЂbЁЂcЪЧRtЁїABCЕФШ§БпЃЌдђa2b2c2ЃЛ
C.ШєaЁЂbЁЂcЪЧRtЁїABCЕФШ§БпЃЌЁЯA=90ЁуЃЌдђa2b2c2ЃЛ
D.ШєaЁЂbЁЂcЪЧRtЁїABCЕФШ§БпЃЌЁЯC=90ЁуЃЌдђa2b2c2ЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєКЏЪ§y=ЃЈkЉ1ЃЉx|k|+b+1ЪЧе§БШР§КЏЪ§ЃЌдђkКЭbЕФжЕЮЊЃЈ ЃЉ
A.k=ЁР1ЃЌb=Љ1
B.k=ЁР1ЃЌb=0
C.k=1ЃЌb=Љ1
D.k=Љ1ЃЌb=Љ1
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com