
【题目】为降低空气污染,公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年均载客量如表:
A型 | B型 | |
价格(万元/辆) | a | b |
年均载客量(万人/年/辆) | 60 | 100 |
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元
(1)求购买每辆A型公交车和每辆B型公交车分别多少万元?
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车年均载客总和不少于680万人次,有哪几种购车方案?请你设计一个方案,使得购车总费用最少.
【答案】(1)购买每辆A型公交车100万元,购买每辆B型公交车150万元;(2)购买A型公交车8辆时,购车的总费用最小,为1100万元.
【解析】
(1)根据“购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元”列方程组求解可得;
(2)设购买A型公交车x辆,则购买B型公交车(10-x)辆,根据“总费用不超过1200万元、年均载客总和不少于680万人次”求得x的范围,设购车的总费用为W,列出W关于x的函数解析式,利用一次函数的性质求解可得.
(1)根据题意,得:![]()
解得:![]()
答:购买每辆A型公交车100万元,购买每辆B型公交车150万元;
(2)设购买A型公交车x辆,则购买B型公交车(10x)辆,
根据题意得:![]()
解得:![]()
设购车的总费用为W,
则W=100x+150(10x)=50x+1500,
∵W随x的增大而减小,
∴当x=8时,W取得最小值,最小值为1100万元.


科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s。
⑴连接AQ、CP交于点M,在点P、Q运动的过程中,∠CMQ的大小变化吗?若变化,则说明理由,若不变,请直接写出它的度数;
⑵点P、Q在运动过程中,设运动时间为t,当t为何值时,△PBQ为直角三角形?
⑶如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ的大小变化吗?则说明理由;若不变,请求出它的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作发现:如图,已知△ABC和△ADE均为等腰三角形,AB=AC,AD=AE,将这两个三角形放置在一起,使点B,D,E在同一直线上,连接CE.

(1)如图1,若∠ABC=∠ACB=∠ADE=∠AED=55°,求证:△BAD≌△CAE;
(2)在(1)的条件下,求∠BEC的度数;
拓广探索:(3)如图2,若∠CAB=∠EAD=120°,BD=4,CF为△BCE中BE边上的高,请直接写出EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;(2)如图3,如果α=45°,AB=2,AE=4![]() ,求点G到BE的距离.
,求点G到BE的距离.
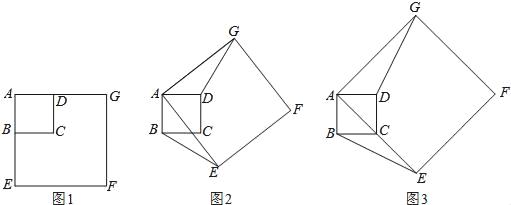
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家新开发的一种摩托车如图所示,它的大灯![]() 射出的光线
射出的光线![]() 、
、![]() 与地面
与地面![]() 的夹角分别为
的夹角分别为![]() 和
和![]() ,大灯
,大灯![]() 离地面距离
离地面距离![]() .
.
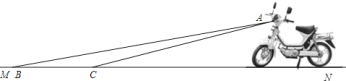
![]() 该车大灯照亮地面的宽度
该车大灯照亮地面的宽度![]() 约是多少(不考虑其它因素)?
约是多少(不考虑其它因素)?
![]() 一般正常人从发现危险到做出刹车动作的反应时间是
一般正常人从发现危险到做出刹车动作的反应时间是![]() ,从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离,某人以
,从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离,某人以![]() 的速度驾驶该车,从
的速度驾驶该车,从![]() 到摩托车停止的刹车距离是
到摩托车停止的刹车距离是![]() ,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.(参考数据:
,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=k1x+b与反比例函数y=![]() 的图象交于第一象限内的P(
的图象交于第一象限内的P(![]() ,8),Q(4,m)两点,与x轴交于A点.
,8),Q(4,m)两点,与x轴交于A点.
(1)分别求出这两个函数的表达式;
(2)写出点P关于原点的对称点P'的坐标;
(3)求∠P'AO的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的动点,将
上的动点,将![]() 沿
沿![]() 折叠.
折叠.
(1)当点![]() 与点
与点![]() 重合时,如图1.若
重合时,如图1.若![]() ,
,![]() ,则
,则![]() 的周长为_____.
的周长为_____.
(2)定义:若在三角形中,期中一条边是另一条边的2倍,则称这个三角形为“倍边三角形”.当点![]() 与点
与点![]() 重合时,如图2.若
重合时,如图2.若![]() ,则
,则![]() 是倍边三角形吗?请说明理由.
是倍边三角形吗?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com