
����Ŀ����֪����ͼ1����A��O��B������ֱ��MN�ϣ��ֽ�����OA�Ƶ�O��˳ʱ�뷽����ÿ��2����ٶ���ת��ͬʱ����OB�Ƶ�O����ʱ�뷽����ÿ��4����ٶ���ת����ͼ2������תʱ��Ϊt��0���t��90�룩��
��1���ú�t�Ĵ���ʽ��ʾ��MOA�Ķ�����
��2�����˶������У�����AOB�ڶ��δﵽ60��ʱ����t��ֵ��
��3������ת�������Ƿ����������t��ʹ������OB��������OM������OA������ON�е�����������ɵĽǣ�ָ����0���������180��Ľǣ���ƽ���ߣ�������ڣ���ֱ��д��t��ֵ����������ڣ���˵�����ɣ�
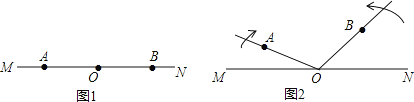
���𰸡���1����MOA=2t����2��t=40��ʱ����AOB�ڶ��δﵽ60�㣻��3����t��ֵ�ֱ�Ϊ18��22.5��36��60��67.5��ʱ������OB��������OM������OA������ON�е�����������ɵĽǵ�ƽ���ߣ�
��������
�����������1����AOM�Ķ�������OA��ת�ٶȳ�����תʱ�䣻
��2������AOB�ڶ��δﵽ60��ʱ������OB��OA����࣬������AOM+��BON����MON=60���з������ɵã�
��3������OB��������OM������OA������ON�е�����������ɵĽǵ�ƽ���������������
��OB����ƽ����AOMʱ������![]() ��AOM=��BOM���з�����⣬
��AOM=��BOM���з�����⣬
��OB����ƽ����MONʱ��������BOM=![]() ��MON���з�����⣬
��MON���з�����⣬
��OBƽ����AONʱ��������BON=![]() ��AON���з�����⣮
��AON���з�����⣮
�⣺��1����MOA=2t��
��2����ͼ��

��������֪����AOM=2t����BON=4t��
����AOB�ڶ��δﵽ60��ʱ����AOM+��BON����MON=60����
��2t+4t��180=60����ã�t=40��
��t=40��ʱ����AOB�ڶ��δﵽ60�㣻
��3������OB��������OM������OA������ON�е�����������ɵĽǵ�ƽ�������������������
��OBƽ����AOMʱ����![]() ��AOM=��BOM��
��AOM=��BOM��
��t=180��4t����t=4t��180��
��ã�t=36��t=60��
��OBƽ����MONʱ���ߡ�BOM=![]() ��MON������BOM=90����
��MON������BOM=90����
��4t=90����4t��180=90��
��ã�t=22.5����t=67.5��
��OBƽ����AONʱ���ߡ�BON=![]() ��AON��
��AON��
��4t=![]() ��180��2t������180����4t��180��=
��180��2t������180����4t��180��=![]() ��180��2t����
��180��2t����
��ã�t=18��t=90�����������⣬��ȥ����
���ϣ���t��ֵ�ֱ�Ϊ18��22.5��36��60��67.5��ʱ������OB��������OM������OA������ON�е�����������ɵĽǵ�ƽ���ߣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У�AB��AC����D�ڵױ�BC�ϣ��������������������ж���ABD�ա�ACD����(����)

A. BD��CD B. ��BAD����CAD C. ��B����C D. ��ADB����ADC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������������A��O��P����O��ԭ�㣬�̶���������A��B�����ƶ�����A��ʾ����Ϊ![]() ����B��ʾ����Ϊ
����B��ʾ����Ϊ![]() .
.
��1����A��B�ƶ�����ͼ��ʾλ�ã�����![]() ��ֵ.
��ֵ.
��2���ڣ�1��������£�B�㲻������A�����ƶ�3����λ����д��A���Ӧ����![]() ��������
��������![]() .
.
��3���ڣ�1��������£���A��������B�����ƶ�15.3����λ������ʱ![]() ��
��![]() ����٣�����ʽ����.
����٣�����ʽ����.
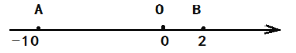
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
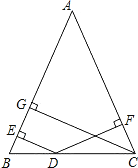
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��D��BC������һ�㣬��D�ֱ���AB��AC�����ߣ�����ֱ�ΪE��F��CG��AB���ϵĸߣ�
��1����D����BC��ʲôλ��ʱ��DE=DF����˵�����ɣ�
��2��DE��DF��CG�ij�֮������������ĵ�����ϵ����˵������.
��3����D�ڵױ�BC���ӳ����ϣ���2���еĽ��ۻ������������������ִ��������Ĺ�ϵ����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ӡ�O��һ��A����O������AB���е�ΪB������AO���ӳ�����O�ڵ�C����D������BC�� 
��1����ͼ1������A=26�㣬���C�Ķ�����
��2����ͼ2����AEƽ�֡�BAC����BC�ڵ�E�����AEB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y=2x��5��x���y��ֱ��ڵ�A�͵�B��������y=��x2+bx+c�Ķ���M��ֱ��AB�ϣ�����������ֱ��AB����һ������ΪN��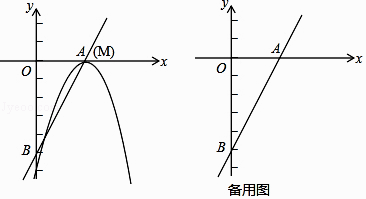
��1����ͼ������M���A�غ�ʱ���������ߵĽ���ʽ��
��2���ڣ�1���������£����N��������߶�MN�ij���
��3��������y=��x2+bx+c��ֱ��AB��ƽ�ƣ��Ƿ���ڵ�M��ʹ�á�OMN���AOB���ƣ������ڣ�ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧ��һԪһ�η��̽ⷨ����ѧ��ʦ����һ���ⷽ����Ŀ��
![]() ������ͬѧ�Ľ��ⲽ�����£�
������ͬѧ�Ľ��ⲽ�����£�
�⣺ȥ��ĸ����3(x��1)��2(2��3x)��1��������
ȥ���ţ���3x��3��4��6x��1�� ������
�����3x��6x��1��3��4�� ������
�ϲ�ͬ����ã�3x��2�� ������
ϵ����Ϊ1����x����![]() �� ������
�� ������
��1����������֪�������Ľ������ڵ�_________(����ţ������˴�������������ԭ����Υ����____.������ţ���ȥ���ŷ��ڵ�ʽ������1���۵�ʽ������2���ܼӷ������ɣ�
��2������д����ȷ�Ľ����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
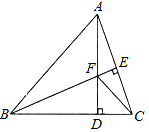
����Ŀ����ͼ����ABC�У�AB=BC��BE��AC�ڵ�E��AD��BC�ڵ�D����BAD=45�㣬AD��BE���ڵ�F������CF��
��1����֤��BF=2AE��
��2����CD=![]() ����AD�ij���
����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
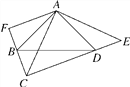
����Ŀ����ͼ����BAD����CAE��90�㣬AB��AD��AE��AC����D��CE�ϣ�AF��CB������ΪF.
(1)��AC��10�����ı���ABCD�������
(2)��֤��CE��2AF.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com