
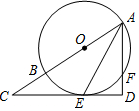
 如图,AB是⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
如图,AB是⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.分析 (1)若要证明CD是⊙O的切线,只需证明CD与半径垂直,故连接OE,证明OE∥AD即可;
(2)分别利用角C的余弦值和正切值,可得出CE和CD,从而即可得出DE的长.
解答 证明:(1)连接OE.
∵OA=OE,
∴∠OAE=∠OEA,
又∵∠DAE=∠OAE,
∴∠OEA=∠DAE,
∴OE∥AD,
∴∠ADC=∠OEC,
∵AD⊥CD,
∴∠ADC=90°,
故∠OEC=90°.
∴OE⊥CD,
∴CD是⊙O的切线.
(2)∵tanC=$\frac{\sqrt{3}}{3}$,
∴∠C=30°,
又∵OE=2,
∴OC=4,AC=6,
在Rt△OCE中,tanC=$\frac{OE}{CE}$,
∴CE=2$\sqrt{3}$,
在Rt△ACD中,cosC=$\frac{CD}{AC}$,
CD=3$\sqrt{3}$
∴DE=CD-CE=3$\sqrt{3}$-2$\sqrt{3}$=$\sqrt{3}$.
点评 本题主要考查了切线的性质和应用,同时也考查了三角函数知识点的应用和平行线的性质,具有一定的综合性,但难度不是太大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费的办法收费.即一个月用水10吨以内(包括10吨)的用户,每吨收水费a元;一个月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图:
我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费的办法收费.即一个月用水10吨以内(包括10吨)的用户,每吨收水费a元;一个月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
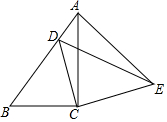 如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕直角顶点C顺时针旋转得到△EDC,此时点B的对应点D恰好落在边AB上,连接AE,则AE的长为$\frac{12}{5}$.
如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕直角顶点C顺时针旋转得到△EDC,此时点B的对应点D恰好落在边AB上,连接AE,则AE的长为$\frac{12}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com