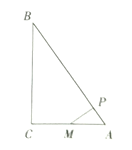
【题目】如图，在△ABC中，∠C=90°，AM=CM，MP⊥AB于点P.求证：BP2=AP2+BC2.
【答案】证明见解析
【解析】
在直角三角形中，连接BM，利用勾股定理得到AB2-AC2+（AM2-MP2）=BC2+（MC2-MP2）①，AM2-MP2=AP2②，MC2+BC2-MP2=BM2-MP2=BP2③．把②③代入①证得结论．
连接BM，如图，
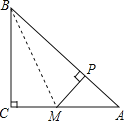
∵△ABC是直角三角形，∠C=90°，
∴AB2=BC2+AC2，则AB2-AC2=BC2．
又∵在直角△AMP中，AP2=AM2-MP2，
∴AB2-AC2+（AM2-MP2）=BC2+（AM2-MP2）．
又∵AM=CM，
∴AB2-AC2+（AM2-MP2）=BC2+（MC2-MP2），①
∵△APM是直角三角形，∴AM2=AP2+MP2，则AM2-MP2=AP2，②
∵△BPM与△BCM都是直角三角形，
∴BM2=BP2+MP2=MC2+BC2，
MC2+BC2-MP2=BM2-MP2=BP2，③
把②③代入①，得
AB2-AC2+AP2=BP2，即BP2=AP2+BC2．
科目：初中数学 来源： 题型：
【题目】已知抛物线y=ax2+bx+c与x轴交于A（1，0），B（3，0），与y轴交于C（0，﹣2），顶点为D，点E的坐标为（0，﹣1），该抛物线于BE交于另一点F，连接BC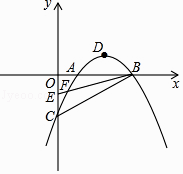
（1）求该抛物线的解析式；
（2）若点H（1，y）在BC上，连接FH，求△FHB的面积；
（3）一动点M从点D出发，以每秒1个单位的速度沿平行于y轴方向向上运动，连接OM，BM，设运动时间为t秒（t＞0），点M在运动过程中，当t为何值时，∠OMB=90°？
（4）在x轴上方的抛物线上，是否存在点P，使得∠PBF被BA平分？若存在，直接写出点P的坐标；若不存在，请说明利由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】A、B两地相距400km，甲、乙两车分别从A、B两地同时出发，相向而行，甲车以每小时100km的速度匀速行驶1h后，休息了1h，然后按原速继续行驶到B地，乙车以每小时80km的速度匀速行驶到A地．
（1）当乙车经过甲车休息的地方时，乙车行驶的时间是 h；
（2）当甲、乙两车相遇时，求乙车行驶的时间；
（3）当甲、乙两车相距40km时，求乙车行驶的时间．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先阅读下列一段文字，再回答问题：
已知平面内两点P1(x1，y1)、P2(x2，y2)，这两点间的距离P1P2＝
．同时当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时，两点间的距离公式可简化为|x2﹣x1|或|y2﹣y1|．
(1)已知点A(2，3)、B(4，2)，试求A、B两点间的距离；
(2)已知点A、B在平行于x轴的直线上，点A的横坐标为7，点B的横坐标为5，试求A、B两点间的距离；
(3)已知一个三角形的各顶点坐标为A(﹣2，1)、B(1，4)、C(1﹣a，5)，试用含a的式子表示△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲箱内有4颗球，颜色分别为红、黄、绿、蓝；乙箱内有3颗球，颜色分别为红、黄、黑．小赖打算同时从甲、乙两个箱子中各抽出一颗球，若同一箱中每球被抽出的机会相等，则小赖抽出的两颗球颜色相同的机率为何？（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，圆O通过五边形OABCD的四个顶点．若 
=150°，∠A=65°，∠D=60°，则 
的度数为何？（ ） 
A.25
B.40
C.50
D.55
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，M、E、F三点在 
上，N是矩形两对角线的交点．若 
=24， =32， 
=16， 
=8， 
=7，则下列哪一条直线是A、C两点的对称轴？（ ）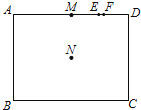 
A.直线MN
B.直线EN
C.直线FN
D.直线DN
查看答案和解析>>
科目：初中数学 来源： 题型：
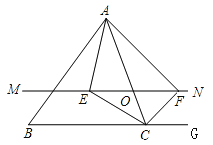
【题目】如图，在△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的角平分线于点E，交∠BCA的外角平分线于点F．
（1）求证：EO=FO；
（2）当点O运动到何处时，四边形AECF是矩形？并证明你的结论．
（3）当点O运动到何处，且△ABC满足什么条件时，四边形AECF是正方形？并说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
