
【题目】观察下列等式的规律,解答下列问题:
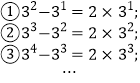
(1)按此规律,第④个等式为_________;第![]() 个等式为_______;(用含
个等式为_______;(用含![]() 的代数式表示,
的代数式表示,![]() 为正整数)
为正整数)
(2)按此规律,计算:
![]()
![]()
【答案】(1)2×34,2×3n;(2)①726;②![]() (3n+1-3).
(3n+1-3).
【解析】
(1)对比列式中的规律变化,找到算式和序号的规律即可求解;
(2)找到算式规律,根据错位相减的方法即可求解.
(1)由题意得:
第④个等式为:35-34=2×34,
第n个等式为:3n+1-3n=2×3n,
故答案为:35-34=2×34, 3n+1-3n=2×3n.
(2)
①2×31+2×32+2×33+2×34+2×35
=32-3+33-32+34-33+35-34+36-35
=36-3
=726.
②31+32+33+···+3n
=![]() (32-3)+
(32-3)+![]() (33-32)+
(33-32)+![]() (34-33)+···+
(34-33)+···+![]() (3n+1-3n)
(3n+1-3n)
=![]() (32-3+33-32+34-33+···+3n+1-3n)
(32-3+33-32+34-33+···+3n+1-3n)
=![]() (3n+1-3).
(3n+1-3).
故答案为:①726, ②![]() (3n+1-3).
(3n+1-3).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
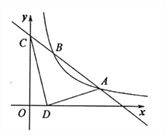
【题目】如图,已知一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求反比例函数和一次函数的表达式.
(2)若在![]() 轴上有一点
轴上有一点![]() ,其横坐标是1,连接
,其横坐标是1,连接![]() 、
、![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为D. 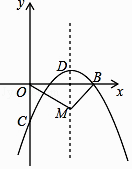
(1)求抛物线的解析式;
(2)一动点M从点D出发,以每秒1个单位的速度沿抛物线的对称轴向下运动,连OM,BM,设运动时间为t秒(t=0),在点M的运动过程中,当∠OMB=90°时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是矩形,cot∠ADB= ![]() ,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.
,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.
(1)求线段BD的长;
(2)设BE=x,△DEF的面积为y,求y关于x的函数关系式,并写出函数定义域;
(3)当△DEF为等腰三角形时,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有30箱苹果,以每箱20千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质质量的差 (单位:千克) |
|
|
| 1 | 2 |
箱数 | 2 | 6 | 10 | 8 | 4 |
(1)这30箱苹果中,最重的一箱比最轻的一箱重多少千克?
(2)与标准质量比较,这30箱苹果总计超过或不足多少千克?
(3)若苹果每千克售价6元,则出售这30箱苹果可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )

A. 2对 B. 3对 C. 4对 D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,BF是AC边上中线,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,当△AEF周长最小时,∠CFE的大小是( )

A. 30° B. 45° C. 60° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E. 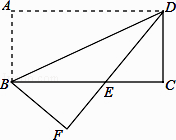
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)x2y﹣3xy2+2x2y﹣y2x ;(2)2(2a2﹣9b)﹣3(3a2﹣7b);
(3)2a2﹣[![]() (ab﹣4a2)+8ab]﹣
(ab﹣4a2)+8ab]﹣![]() ab.
ab.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com