Question

在直角△ABC中，∠C=90°，直角边BC与直角坐标系中的x轴重合，其内切圆的圆心坐标为P（0，1），若抛物线y=kx²+2kx+1的顶点为A．求：
（1）求抛物线的对称轴、顶点坐标和开口方向；
（2）用k表示B点的坐标；
（3）当k取何值时，∠ABC=60°？

Answer 1

分析：（1）对二次函数式进行变形，可得y=k（x+1）²+（1-k），即得顶点坐标A（-1，1-k），对称轴就是x=-1，又x=0时，y=1，说明函数经过（0，1），也就是二次函数的开口必然向下，即k＜0；
（2）用k的代数式分别表示AC、BC、AB，利用勾股定理可得相等关系，可求出OB，即得B点坐标；
（3）在Rt△ABC中利用∠ABC的正切值，可求出k的值，注意k＜0．

解答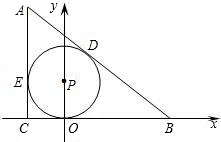：解：（1）∵y=kx²+2kx+1
∴对称轴x=-1，易见抛物线是以Rt△ABC的直角边AC所在直线为对称轴，
由题易得A（-1，1-k），又当x=0时，y=1
即抛物线过p（0，1），
故k＜0开口向下．（4分）

（2）如图，
AC=1-K  BC=CO+OB=1+OB AB=AD+BD=AE+OB=AC-CE+OB=OB-k
由勾股定理得（1-k）²+（1+OB）²=（OB-k）²?OB=

k-1

k+1

?B(

k-1

k+1

，0)（4分）

（3）∵∠ABC=60°，
∴tan∠ABC=

3

又tan∠ABC=

1-k2

2k

=

3

∴k2+2

3

k-1=0
∴k^=-

3

+2，k2=-

3

-2
又∵k＜0
∴k=-

3

-2．（4分）

点评：本题利用了二次函数的解析式可以变形，勾股定理，以及三角函数，解一元二次方程等知识．