
【题目】某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如图的统计表和扇形图:

各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 20 |
B | b | 18 |
C | c | 15 |
(1)①在扇形图中,a= ,C部门所对应的圆心角的度数为 .
②在统计表中,b= ,c= .
(2)求这个公司平均每人所创年利润.
【答案】(1)①25、108°;②9、6;(2)这个公司平均每人所创年利润为17.6(万元).
【解析】
(1)①根据扇形圆心角的度数=部分占总体的百分比×360°进行计算即可;②先求得A部门的员工人数所占的百分比,进而得到各部门的员工总人数,据此可得B,C部门的人数;
(2)根据总利润除以总人数,即可得到这个公司平均每人所创年利润.
解:(1)①在扇形图中,a=100﹣45﹣30=25,C部门所对应的圆心角的度数为360 ![]() ×30%=108
×30%=108 ![]() ,
,
故答案为:25、108 ![]() .
.
②∵总人数为5÷25%=20人,
∴b=20×45%=9、c=20×30%=6,
故答案为:9、6;
(2)这个公司平均每人所创年利润为![]() =17.6(万元).
=17.6(万元).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
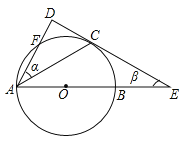
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是上半圆的弦,过点
是上半圆的弦,过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作切线
作切线![]() 的垂线,垂足为
的垂线,垂足为![]() ,且与
,且与![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() 的度数分别是
的度数分别是![]() .
.
![]() 用含
用含![]() 的代数式表示
的代数式表示![]() ,并直接写出
,并直接写出![]() 的取值范围;
的取值范围;
![]() 连接
连接![]() 与
与![]() 交于点
交于点![]() ,当点
,当点![]() 是
是![]() 的中点时,求
的中点时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“ 亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
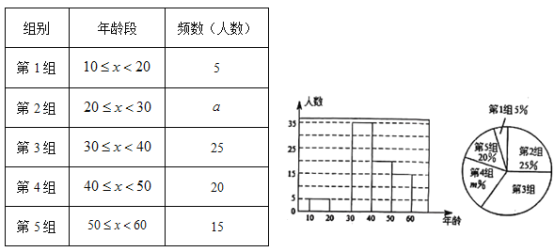
(1)请直接写出![]() _______,
_______,![]() _______,第3组人数在扇形统计图中所对应的圆心角是_______度.
_______,第3组人数在扇形统计图中所对应的圆心角是_______度.
(2)请补全上面的频数分布直方图.
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:已知点![]() 是三角形边上的一点(顶点除外),若它到三角形一条边的距离等于它到三角形的一个顶点的距离,则我们把点
是三角形边上的一点(顶点除外),若它到三角形一条边的距离等于它到三角形的一个顶点的距离,则我们把点![]() 叫做该三角形的等距点.
叫做该三角形的等距点.
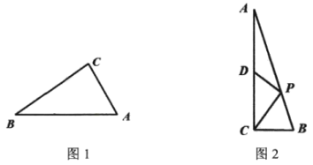
(1)如图1:![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 在斜边
在斜边![]() 上,且点
上,且点![]() 是
是![]() 的等距点,试求
的等距点,试求![]() 的长;
的长;
(2)如图2,![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,
,![]() 为
为![]() 中点,且
中点,且![]() .
.
①求证:![]() 的外接圆圆心是
的外接圆圆心是![]() 的等距点;②求
的等距点;②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
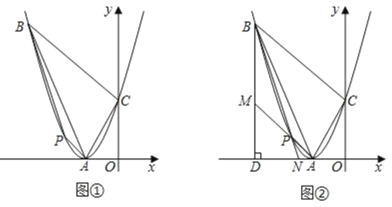
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的顶点为A(﹣2,0),且经过点B(﹣5,9),与y轴交于点C,连接AB,AC,BC.
(1)求该抛物线对应的函数表达式;
(2)点P为该抛物线上点A与点B之间的一动点.
①若S△PAB=![]() S△ABC,求点P的坐标.
S△ABC,求点P的坐标.
②如图②,过点B作x轴的垂线,垂足为D,连接AP并延长,交BD于点M.连接BP并延长,交AD于点N.试说明DN(DM+DB)为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
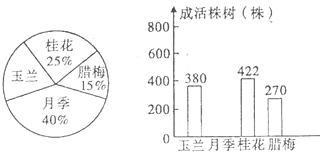
【题目】“不出城郭而获山水之怡,身居闹市而有林泉之致”,合肥市某区不断推进“园林城市”建设,今春种植了四类花苗,园林部门从种植的这批花苗中随机抽取了2000株,将四类花苗的种植株数绘制成扇形统计图,将四类花苗的成活株数绘制成条形统图.经统计这批2000株的花苗总成活率为90%,其中玉兰和月季的成活率较高,根据图表中的信息解答下列问题:
(1)扇形统计图中玉兰所对的圆心角为 ,并补全条形统计图;
(2)该区今年共种植月季8000株,成活了约 株;
(3)园林部门决定明年从这四类花苗中选两类种植,请用列表法或画树状图求恰好选到成活率较高的两类花苗的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一种折叠台灯,将其放置在水平桌面上,图2是其简化示意图,测得其灯臂![]() 长为
长为![]() 灯翠
灯翠![]() 长为
长为![]() ,底座
,底座![]() 厚度为
厚度为![]() 根据使用习惯,灯臂
根据使用习惯,灯臂![]() 的倾斜角
的倾斜角![]() 固定为
固定为![]() ,
,
(1)当![]() 转动到与桌面平行时,求点
转动到与桌面平行时,求点![]() 到桌面的距离;
到桌面的距离;
(2)在使用过程中发现,当![]() 转到至
转到至![]() 时,光线效果最好,求此时灯罩顶端
时,光线效果最好,求此时灯罩顶端![]() 到桌面的高度(参考数据:
到桌面的高度(参考数据:![]() ,结果精确到个位).
,结果精确到个位).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:
①∠APB=120°;②AF+BE=AB.
那么,当AM∥BN时:
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出∠APB的度数,写出AF,BE,AB长度之间的等量关系,并给予证明;
(2)设点Q为线段AE上一点,QB=5,若AF+BE=16,四边形ABEF的面积为32![]() ,求AQ的长.
,求AQ的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com