
平面上有![]() 个点(
个点(![]() ,
,![]() 为自然数),其中任何三点不在同一直线上。证明:一定存在三点,以这三点作为顶点的三角形中至少有一个内角不大于
为自然数),其中任何三点不在同一直线上。证明:一定存在三点,以这三点作为顶点的三角形中至少有一个内角不大于![]() 。
。
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
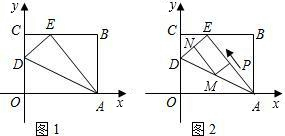
 AB边上,记为D点,AE为折痕,E在y轴上.
AB边上,记为D点,AE为折痕,E在y轴上.查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| x |
| 9-x |
| 10 |
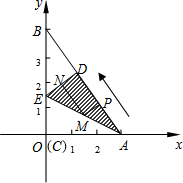
 上的点E处.
上的点E处.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012届福建省泉州三中九年级下学期第一次质量检查数学卷 题型:解答题
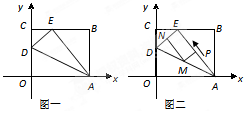
(14分)如图一, 是一张放在平面直角坐标系中的矩形纸片,
是一张放在平面直角坐标系中的矩形纸片, 为原点,点
为原点,点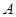 在
在 轴的正半轴上,点
轴的正半轴上,点 在
在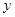 轴的正半轴上,
轴的正半轴上, ,
, .
.
(1)在 边上取一点
边上取一点 ,将纸片沿
,将纸片沿 翻折,使点
翻折,使点 落在
落在 边上的点
边上的点 处,求
处,求 两点的坐标;
两点的坐标;
(2)如图二,若 上有一动点
上有一动点 (不与
(不与 重合)自
重合)自 点沿
点沿 方向向
方向向 点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为
点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为 秒(
秒(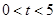 ),过
),过 点作
点作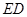 的平行线交
的平行线交 于点
于点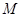 ,过点
,过点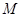 作
作 的平行线交
的平行线交 于点
于点 .求四边形
.求四边形 的面积
的面积 与时间
与时间 之间的函数关系式;当
之间的函数关系式;当 取何值时,
取何值时, 有最大值?最大值是多少?
有最大值?最大值是多少?
(3)在(2)的条件下,当 为何值时,以
为何值时,以 为顶点的三角形为等腰三角形,并求出相应的时刻点
为顶点的三角形为等腰三角形,并求出相应的时刻点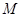 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com