
| 型号 | 进价(元/只) | 售价(元/只) |
| A型 | 12 | 18 |
| B型 | 15 | 23 |
分析 (1)由该文具店购进A种型号的文具x只,可得知购进B种型号的文具(100-x)只,根据总利润=单只利润×购进数量,即可得出y关于x的函数关系式;
(2)由实际进货时进货款不得超过1380元,可得出关于x的一元一次不等式,解之即可得出x的取值范围,再根据一次函数的性质,即可解决最值问题.
解答 解:(1)该文具店购进A种型号的文具x只,则购进B种型号的文具(100-x)只,
根据题意得:y=(18-12)x+(23-15)(100-x)=-2x+800.
(2)根据题意得:12x+15(100-x)≤1380,
解得:x≥40.
∵在y=-2x+800中,-2<0,
∴y随x的增大而减小,
∴当x=40时,y取最大值,最大值为720.
答:该文具店销售完这批文具后所能获得最大利润为720元.
点评 本题考查了一次函数的应用、一元一次不等式的应用以及一次函数的性质,解题的关键是:(1)根据总利润=单只利润×购进数量,找出y关于x的函数关系式;(2)根据实际进货时进货款不得超过1380元,列出关于x的一元一次不等式.


科目:初中数学 来源: 题型:填空题
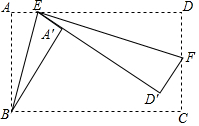 如图,矩形ABCD中,AB=8,BC=15,点E是AD边上一点,连接BE,把△ABE沿BE折叠,使点A落在点A′处,点F是CD边上一点,连接EF,把△DEF沿EF折叠,使点D落在直线EA′上的点D′处,当点D′落在BC边上时,AE的长为$\frac{15+\sqrt{33}}{3}$或$\frac{15-\sqrt{33}}{3}$.
如图,矩形ABCD中,AB=8,BC=15,点E是AD边上一点,连接BE,把△ABE沿BE折叠,使点A落在点A′处,点F是CD边上一点,连接EF,把△DEF沿EF折叠,使点D落在直线EA′上的点D′处,当点D′落在BC边上时,AE的长为$\frac{15+\sqrt{33}}{3}$或$\frac{15-\sqrt{33}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
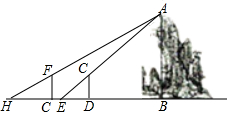 假山具有多方面的造景功能,与建筑、植物等组合成富于变化的景致.某公园有一座假山,小亮、小慧等同学想用一些测量工具和所学的几何知识测量这座假山的高度来检验自己掌握知识和运用知识的能力,如图,在阳光下,小亮站在水平地面的D处,此时小亮身高的影子顶端与假山的影子顶端E重合,这时小亮身高CD的影长DE=2米,一段时间后,小亮从D点沿BD的方向走了3.6米到达G处,此时小亮身高的影子顶端与假山的影子顶端H重合,这时小亮身高的影长GH=2.4米,已知小亮的身高CD=FG=1.5米,点G、E、D均在直线BH上,AB⊥BH,CD⊥BH,GF⊥BH,请你根据题中提供的相关信息,求出假山的高度AB.
假山具有多方面的造景功能,与建筑、植物等组合成富于变化的景致.某公园有一座假山,小亮、小慧等同学想用一些测量工具和所学的几何知识测量这座假山的高度来检验自己掌握知识和运用知识的能力,如图,在阳光下,小亮站在水平地面的D处,此时小亮身高的影子顶端与假山的影子顶端E重合,这时小亮身高CD的影长DE=2米,一段时间后,小亮从D点沿BD的方向走了3.6米到达G处,此时小亮身高的影子顶端与假山的影子顶端H重合,这时小亮身高的影长GH=2.4米,已知小亮的身高CD=FG=1.5米,点G、E、D均在直线BH上,AB⊥BH,CD⊥BH,GF⊥BH,请你根据题中提供的相关信息,求出假山的高度AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4×108 | B. | 4×10-8 | C. | 0.4×108 | D. | -4×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
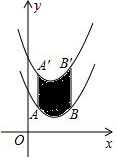 如图,将函数y=$\frac{1}{2}$(x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
如图,将函数y=$\frac{1}{2}$(x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )| A. | $y=\frac{1}{2}{({x-2})^2}-2$ | B. | $y=\frac{1}{2}{({x-2})^2}+7$ | C. | $y=\frac{1}{2}{({x-2})^2}-5$ | D. | $y=\frac{1}{2}{({x-2})^2}+4$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com