
【题目】综合与实践
背景阅读 早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”.它被记载于我国古代著名数学著作《周髀算经》中,为了方便,在本题中,我们把三边的比为3:4:5的三角形称为(3,4,5)型三角形,例如:三边长分别为9,12,15或3 ![]() ,4
,4 ![]() ,5
,5 ![]() 的三角形就是(3,4,5)型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
的三角形就是(3,4,5)型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
实践操作 如图1,在矩形纸片ABCD中,AD=8cm,AB=12cm.
第一步:如图2,将图1中的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB上的点E处,折痕为AF,再沿EF折叠,然后把纸片展平.
第二步:如图3,将图2中的矩形纸片再次折叠,使点D与点F重合,折痕为GH,然后展平,隐去AF.
第三步:如图4,将图3中的矩形纸片沿AH折叠,得到△AD′H,再沿AD′折叠,折痕为AM,AM与折痕EF交于点N,然后展平.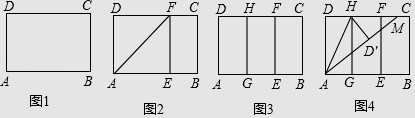
(1)请在图2中证明四边形AEFD是正方形.
(2)请在图4中判断NF与ND′的数量关系,并加以证明;
(3)请在图4中证明△AEN(3,4,5)型三角形;
(4)在不添加字母的情况下,图4中还有哪些三角形是(3,4,5)型三角形?请找出并直接写出它们的名称.
【答案】
(1)
证明:∵四边形ABCD是矩形,
∴∠D=∠DAE=90°,
由折叠的性质得,AE=AD,∠AEF=∠D=90°,
∴∠D=∠DAE=∠AEF=90°,
∴四边形AEFD是矩形,
∵AE=AD,
∴矩形AEFD是正方形
(2)
解:NF=ND′,
理由:连接HN,
由折叠得,∠AD′H=∠D=90°,HF=HD=HD′,
∵四边形AEFD是正方形,
∴∠EFD=90°,
∵∠AD′H=90°,
∴∠HD′N=90°,
在Rt△HNF与Rt△HND′中, ![]() ,
,
∴Rt△HNF≌Rt△HND′,
∴NF=ND′
(3)
解:∵四边形AEFD是正方形,
∴AE=EF=AD=8cm,
由折叠得,AD′=AD=8cm,
设NF=xcm,则ND′=xcm,
在Rt△AEN中,
∵AN2=AE2+EN2,
∴(8+x)2=82+(8﹣x)2,
解得:x=2,
∴AN=8+x=10cm,EN=6cm,
∴EN:AE:AN=3:4:5,
∴△AEN是(3,4,5)型三角形
(4)
解:图4中还有△MFN,△MD′H,△MDA是(3,4,5)型三角形,
∵CF∥AE,
∴△CFN∽△AEN,
∵EN:AE:AN=3:4:5,
∴FN:CF:CN=3:4:5,
∴△MFN是(3,4,5)型三角形;
同理,△MD′H,△MDA是(3,4,5)型三角形.
【解析】(1)根据矩形的性质得到∠D=∠DAE=90°,由折叠的性质得得到AE=AD,∠AEF=∠D=90°,求得∠D=∠DAE=∠AEF=90°,得到四边形AEFD是矩形,由于AE=AD,于是得到结论;(2)连接HN,由折叠的性质得到∠AD′H=∠D=90°,HF=HD=HD′,根据正方形的想知道的∠HD′N=90°,根据全等三角形的性质即可得到结论;(3)根据正方形的性质得到AE=EF=AD=8cm,由折叠得,AD′=AD=8cm,设NF=xcm,则ND′=xcm,根据勾股定理列方程得到x=2,于是得到结论;(4)根据(3,4,5)型三角形的定义即可得到结论.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对相似三角形的应用的理解,了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】观察图,回答下列问题:
(1)甲、乙两图分别能折成什么几何体?简述它们的特征;
(2)设几何体的面数为F,顶点数为V,棱数为E,请计算(1)中两个几何体的F+V-E的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
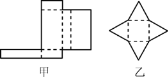
【题目】小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.
(1)若区域Ⅰ的三种瓷砖均价为300元/m2 , 面积为S(m2),区域Ⅱ的瓷砖均价为200元/m2 , 且两区域的瓷砖总价为不超过12000元,求S的最大值;
(2)若区域Ⅰ满足AB:BC=2:3,区域Ⅱ四周宽度相等
①求AB,BC的长;
②若甲、丙两瓷砖单价之和为300元/m2 , 乙、丙瓷砖单价之比为5:3,且区域Ⅰ的三种瓷砖总价为4800元,求丙瓷砖单价的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题.
 程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
在《算法统宗》里记载了一道趣题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD=CD,∠ABD=∠ACD=90°,点E、F分别在AB、AC上,若ED平分∠BEF.
(1)求证:FD平分∠EFC.
(2)若EF=4,AF=6,AE=5,求BE和CF的和的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿东北方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,停留半小时后再转向北偏东30°方向开往B岛,其速度仍为20海里/小时.
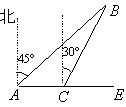
(1)求港口A到海岛B的距离;
(2)B岛建有一座灯塔,在离灯塔方圆5海里内都可以看见灯塔,问甲、乙两船哪一艘先看到灯塔?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为6的正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数y= ![]() 位于第一象限的图象上,则k的值为( )
位于第一象限的图象上,则k的值为( ) 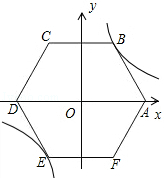
A.9 ![]()
B.9 ![]()
C.3 ![]()
D.3 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com