练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AB是半圆的直径，C、D是半圆上的两点，且∠BAC=20°，．请连结线段CB，求四边形ABCD各内角的度数．

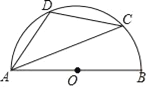
    【答案】55°，70°，125°，110°

    【解析】试题分析：连结BC，根据圆周角定理得∠ACB=90°，则利用互余可计算出∠B=70°，再根据圆内接四边形的性质计算出∠D=180°﹣∠B=110°，接着根据圆周角定理和三角形内角和定理，由弧AD=弧CD得到∠DAC=∠DCA=35°，然后计算∠DAB=∠DAC+∠BAC=55°，∠DCB=∠DCA+∠ACB=125°．

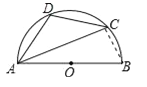
    试题解析：解：连结BC，如图，∵AB是半圆的直径，∴∠ACB=90°，∵∠BAC=20°，∴∠B=70°，∵四边形ABCD是圆O的内接四边形，∴∠D=180°﹣∠B=110°，∵弧AD=弧CD，∴∠DAC=∠DCA=（180°-110°）=35°，∴∠DAB=∠DAC+∠BAC=55°，∠DCB=∠DCA+∠ACB=125°，即四边形ABCD各内角的度数分别为55°，70°，125°，110°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

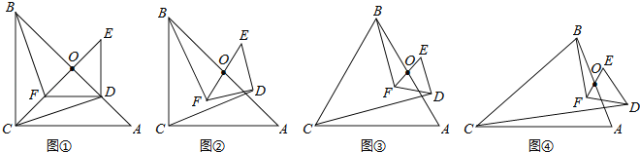
    【题目】如图①，△ABC与△DEF都是等腰直角三角形，∠ACB=∠EDF=90°，且点D在AB边上，AB、EF的中点均为O，连结BF、CD、CO，显然点C、F、O在同一条直线上，可以证明△BOF≌△COD，则BF=CD．

    解决问题

    （1）将图①中的Rt△DEF绕点O旋转得到图②，猜想此时线段BF与CD的数量关系，并证明你的结论；

    （2）如图③，若△ABC与△DEF都是等边三角形，AB、EF的中点均为O，上述（1）中的结论仍然成立吗？如果成立，请说明理由；如不成立，请求出BF与CD之间的数量关系；

    （3）如图④，若△ABC与△DEF都是等腰三角形，AB、EF的中点均为0，且顶角∠ACB=∠EDF=α，请直接写出的值（用含α的式子表示出来）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某开发区计划在一块四边形的空地ABCD上种植草坪，已知∠A=90°，AB=4m，BC=12m，CD=13m，DA=3m，种植每平方米草皮的预算费用为300元，若第一年对草坪的保养费用占种植草皮总预算的4%，以后每年的保养费用都将在前一年的基础上递增2%，求第三年的草坪保养费用．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市举行知识大赛，A校、B校各派出5名选手组成代表队参加决赛，两校派出选手的决赛成绩如图所示．

    根据图示填写下表：

    平均数分

    中位数分

    众数分

    A校

    ______

    85

    ______

    B校

    85

    ______

    100

    结合两校成绩的平均数和中位数，分析哪个学校的决赛成绩较好；

    计算两校决赛成绩的方差，并判断哪个学校代表队选手成绩较为稳定．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB=3，BC=4，O为矩形ABCD的中心，以D为圆心1为半径作⊙D，P为⊙D上的一个动点，连接AP、OP，则△AOP面积的最大值为（　　）

    A. 4 B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x，y的方程组

    （1）若a=2，请直接写出此时方程组的解；

    （2）若方程组的解满足x+y=6，求a的值；

    （3）若方程组的解x，y的值都为非负数，求2x-y的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四幅图象分别表示变量之间的关系，请按图象的顺序，将下面的四种情境与之对应排序．正确的顺序是（　　）

    ①篮球运动员投篮时，投出去的篮球的高度与时间的关系；

    ②去超市购买同一单价的水果，所付费用与水果数量的关系；

    ③李老师使用的是一种含月租的手机计费方式，则他每月所付话费与通话时间的关系；

    ④周末，小明从家到图书馆，看了一段时间书后，按原速度原路返回，小明离家的距离与时间的关系

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

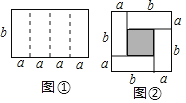
    【题目】如图①是一个长为4a、宽为b的长方形，沿图中虚线用剪刀将其平均分成四块小长方形，然后用四块小长方形拼成一个“回形”正方形（如图②）

    自主探索：

    （1）仔细观察图形，完成下列问题

    ①图②中的阴影部分的面积为_____；

    ②观察图②，请你写出（a+b）2、（a-b）2、ab之间的等量关系是_____；

    知识运用：

    （2）若x-y=5，xy=，根据（1）中的结论，求（x+y）2的值；

    知识延伸

    （3）根据你探索发现的结论，完成下列问题：

    设A=，B=x+2y-3

    计算（A-B）2-（A+B）2的结果．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】盒中有若干枚黑棋和白棋，这些棋除颜色外无其他差别，现让学生进行摸棋试验：每次摸出一枚棋，记录颜色后放回摇匀，重复进行这样的试验得到以下数据：

    摸棋的次数n

    100

    200

    300

    500

    800

    1000

    摸到黑棋的次数m

    24

    51

    76

    b

    201

    250

    摸到黑棋的频率（精确到0.001）

    0.240

    a

    0.253

    0.248

    0.251

    0.250

    （1）填空：a=　 　，b=　 　；

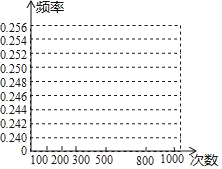
    （2）在图中，画出摸到黑棋的折线统计图；

    （3）随机摸一次，估计摸到黑棋的概率．（精确到0.01）

    查看答案和解析>>

    同步练习册答案