
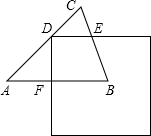
 如图,在△ABC中,AB=AC=1,∠A=60°,边长为1的正方形的一个顶点D在边AC上,与△ABC另两边分别交于点E、F,DE∥AB,将正方形平移,使点D保持在AC上(D不与A重合),设AF=x,正方形与△ABC重叠部分的面积为y.
如图,在△ABC中,AB=AC=1,∠A=60°,边长为1的正方形的一个顶点D在边AC上,与△ABC另两边分别交于点E、F,DE∥AB,将正方形平移,使点D保持在AC上(D不与A重合),设AF=x,正方形与△ABC重叠部分的面积为y.分析 1)当点D保持在AC上时,正方形与△ABC重叠部分为直角梯形DEBF,根据直角梯形的面积公式,只需用含x的代数式分别表示出上底DE、下底BF及高DF的长度即可.由△ADF为等腰直角三角形,可得高DF=AF=x;则AD=2x,下底BF=AB-AF=1-x;进而得出CD,再根据等腰三角形及平行线的性质可证∠C=∠CED,得出上底DE根据点D保持在AC上,且D不与A重合,可知0<AD≤1,从而求出自变量x的取值范围;
(2)由(1)知,y是x的二次函数,根据二次函数的性质,即可得到结论.
解答 解:(1)∵AB=AC,
∴∠B=∠C,
∵DE∥AB,
∴∠B=∠CED,∠AFD=∠FDE=90°,
∴∠C=∠CED,
∴DC=DE.(2分)
在Rt△ADF中,∵∠A=60°,
∴∠ADF=60°=∠A,
∴AF=x,
∴AD=$\frac{x}{cos60°}$=2x,DF=$\sqrt{3}$x,DM=$\frac{\sqrt{3}}{2}$,
∴DC=DE=1-2x,
∴y=$\frac{1}{2}$(DE+FB)×DF=$\frac{1}{2}$(1-2x+1-x)$\sqrt{3}$x=-$\frac{2}{3}$$\sqrt{3}$x2+$\sqrt{3}$x.
∵点D保持在AC上,且D不与A重合,
∴0<AD≤1,
∴0<$\frac{1}{2}$x≤1,
∴0<x≤$\frac{\sqrt{3}}{2}$.
故y=-$\frac{2}{3}$$\sqrt{3}$x2+$\sqrt{3}$x,自变量x的取值范围是0<x≤$\frac{\sqrt{3}}{2}$;
(2)∵y=-$\frac{2}{3}$$\sqrt{3}$x2+$\sqrt{3}$x,
∴当x=$\frac{1}{3}$时,y有最大值是$\frac{\sqrt{3}}{6}$.
点评 本题考查了正方形、平行线的性质,等腰三角形的性质与判定,直角梯形的面积及二次函数的性质,综合性较强,难度中等.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
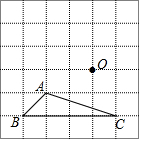 如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上)
如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
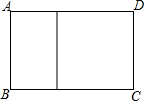 如图,用长120cm的木条制成如图形状的矩形框(矩形框中间有一横档).设矩形框的宽AB为x(cm),所围成的面积为S(cm2).
如图,用长120cm的木条制成如图形状的矩形框(矩形框中间有一横档).设矩形框的宽AB为x(cm),所围成的面积为S(cm2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … |
| 分割成的三角形的个数 | 4 | 6 | 8 | 10 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知∠ABC=∠ADC,BE,DF分别平分∠ABC,∠ADC,且∠1=∠2,请说明:∠A=∠C.
如图,已知∠ABC=∠ADC,BE,DF分别平分∠ABC,∠ADC,且∠1=∠2,请说明:∠A=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com