
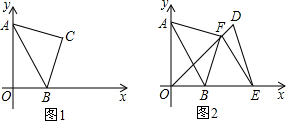
分析 (1)①根据非负数的性质列出算式,求出a、b的值;
②根据等腰直角三角形的性质求出AC、BC,根据三角形的面积公式计算即可;
(2)作FG⊥y轴,FH⊥x轴垂足分别为G、H,证明四边形FHOG是正方形,得到OG=FH,∠GFH=90°,证明△AFG≌△BFH,根据全等三角形的性质计算即可.
解答 解:(1)①∵a2+b2-8a-4b+20=0,
∴(a-4)2+(b-2)2=0,
∴a=4,b=2;
②∵A(0,4),B(2,0),
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2$\sqrt{5}$,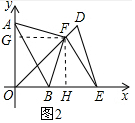
∵△ABC是等腰直角三角形,
∴AC=BC=$\sqrt{10}$,
∴四边形AOBC的面积S=$\frac{1}{2}$×OA×OB+$\frac{1}{2}$×AC×BC=4+5=9;
(2)结论:FA=FB,FA⊥FB,理由如下:
如图2,作FG⊥y轴,FH⊥x轴垂足分别为G、H,
∵A(0,a)向右平移a个单位到D,
∴点D坐标为(a,a),点E坐标为(a+b,0),
∴∠DOE=45°,
∵EF⊥OD,
∴∠OFE=90°,∠FOE=∠FEO=45°,
∴FO=EF,
∴FH=OH=HE=$\frac{1}{2}$(a+b),
∴点F坐标为($\frac{a+b}{2}$,$\frac{a+b}{2}$),
∴FG=FH,四边形FHOG是正方形,
∴OG=FH=$\frac{a+b}{2}$,∠GFH=90°,
∴AG=AO-OG=a-$\frac{a+b}{2}$=$\frac{a-b}{2}$,BH=OH-OB=$\frac{a+b}{2}$-b=$\frac{a-b}{2}$,
∴AG=BH,
在△AFG和△BFH中,
$\left\{\begin{array}{l}{AG=BH}\\{∠AGF=∠BHF}\\{FG=FH}\end{array}\right.$,
∴△AFG≌△BFH,
∴FA=FB,∠AFG=∠BFH,
∴∠AFB=∠AFG+∠BFG=∠BFH+∠BFG=90°,
∴FA=FB,FA⊥FB.
点评 本题考查全等三角形的判定和性质、勾股定理、非负数的性质,解题的关键是掌握平移的性质、正确添加辅助线构造全等三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,OA是北偏东30°方向的一条射线,若∠AOB=90°,则OB的方向角是( )
如图,OA是北偏东30°方向的一条射线,若∠AOB=90°,则OB的方向角是( )| A. | 北偏西30° | B. | 北偏西60° | C. | 东偏北30° | D. | 东偏北60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2-(-4a+3)=a2+4a+3 | B. | a2+(-3-4a)=a2-3+4a | ||
| C. | (a-3b)-(4c-2)=a-3b-4c+2 | D. | a-(c-d)=a-c-d |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE,则∠AEB的度数是( )
如图,△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE,则∠AEB的度数是( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查一批汽车的使用寿命 | |
| B. | 调查山东省市民春节期间计划外出旅游情况 | |
| C. | 调查某航班的旅客是否携带了违禁物品 | |
| D. | 调查全国初三学生的视力情况 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com