练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
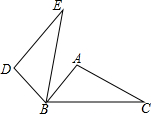
    3．如图，△ABC中，∠ABC=40°，∠C=30°，将△ABC绕点B逆时针旋转α（0°＜α≤90°）得到△DBE，若DE∥AB，则α为（　　）
    A．50°B．70°C．80°D．90°

    分析 先根据旋转的性质得∠E=∠C=30°，∠EBC=α，则根据平行线的性质得∠EBA=∠E=30°，然后计算∠EBA+∠ABC即可．

    解答 解：∵△ABC绕点B逆时针旋转α（0°＜α≤90°）得到△DBE，
    ∴∠E=∠C=30°，∠EBC=α，
    ∵DE∥AB，
    ∴∠EBA=∠E=30°，
    ∴α=∠EBA+∠ABC=30°+40°=70°．
    故选B．

    点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了平行线的性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

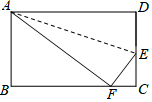    11．如图，在长方形ABCD中，DC=9．在DC上找一点E，沿直线AE把△AED折叠，使D点恰好落在BC上，设这一点为F，若△ABF的面积是54，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．在△ABC中，∠A+∠B=∠C，∠B=2∠A，求∠A、∠B、∠C的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．在坐标系中，点O是坐标原点，抛物线y=-$\frac{1}{12}$x2+k的顶点M，直线y=-$\frac{1}{2}$x+b（b＞0）分别与x轴，y轴交于点A和点B．点是AB的中点
    （1）若点P（$\sqrt{3}$k，1）在抛物线上，求k的值；
    （2）若抛物线y=-$\frac{1}{12}$x2+k经过点A和点B，求点C的坐标；
    （3）把已知抛物线向右平移2个单位得到的新抛物线与直线y=-$\frac{1}{2}$x+b交于第一象限的P，Q两点，若新抛物线顶点恰好为点P，△OCQ的面积记为S，求S的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

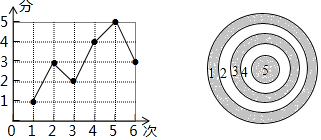    18．一种游戏如图，在一个定点位置用球拍扫动滑块，滑块落在圆环形靶图的相应位置，可以得到相应的分数．江小颖做6次的成绩如左图，对于这组数据，说法中不正确的是（　　）
    A．平均数3B．中位数3C．方差是2.5D．众数是3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况，随机抽取了一部分学生进行调查统计（要求每名学生选出并且只能选出一个自己最喜爱的节目），并将调查结果绘制成如图统计图表：
    学生最喜爱的节目人数统计表
    节目 人数（名） 百分比
     最强大脑 5 10%
     朗读者 15b%
     中国诗词大会 a 40%
     出彩中国人 10 20%
    根据以上提供的信息，解答下列问题：
    （1）a=20，b=30；
    （2）补全上面的条形统计图；
    （3）若该校共有学生1600名，根据抽样调查结果，估计该校最喜爱《朗读者》节目的学生有多少名．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列关系式正确的是（　　）
    A．（2a+1）2=2a2+1B．（2a-1）2=4a2-1
    C．（3a+2b）（3a-2b）=9a2-4b2D．（2a-1）2=4a2+4a+1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．解不等式组：$\left\{\begin{array}{l}2（x-6）＞x-10\\ x-1≤\frac{5x-9}{3}\end{array}\right.$，并将其解集表示在数轴上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，一次函数y=$\frac{1}{2}$x-2与反比例函数y=$\frac{m}{x}$的图象交于点A，且点A的纵坐标为1．
    （1）反比例函数的解析式；
    （2）根据图象直接写出当x＞0时，一次函数的值小于反比例函数的值的x的取值范围．

    查看答案和解析>>

    同步练习册答案