
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券 | 5 | 10 | 5 |
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券 | 10 | 5 | 10 |
分析 (1)让所求的情况数除以总情况数即为所求的概率;
(2)算出相应的平均收益,比较即可.
解答 解:(1)树状图: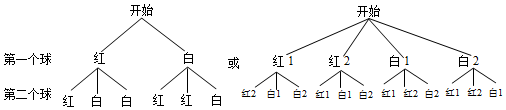
(2)方法1:∵去甲超市购物摸一次奖获10元礼金券的概率P(甲)=$\frac{4}{6}$=$\frac{2}{3}$,
去乙超市购物摸一次奖获10元礼金券的概率P(乙)=$\frac{2}{6}$=$\frac{1}{3}$,
∴P(甲)>P(乙),
∴我选择去甲超市购物;
方法2:∵P(两红)=$\frac{1}{6}$,P(两白)=$\frac{1}{6}$,P(一红一白)=$\frac{2}{3}$,
∴在甲商场获礼金券的平均收益是$\frac{1}{6}$×5+$\frac{2}{3}$×10+$\frac{1}{6}$×5=$\frac{25}{3}$,
在乙商场获礼金券的平均收益是$\frac{1}{6}$×10+$\frac{2}{3}$×5+$\frac{1}{6}$×10=$\frac{20}{3}$,
∴$\frac{25}{3}$>$\frac{20}{3}$,
∴我选择去甲超市购物.
点评 考查了列表法与树状图法,树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:选择题
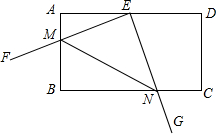 矩形ABCD中,AD=2AB=2$\sqrt{2}$,E是AD的中点,Rt∠FEG顶点与点E重合,将∠FEG绕点E旋转,角的两边分别交AB,BC(或它们的延长线)于点M,N,设∠AME=α(0°<α<90°),有下列结论:①BM=CN;②AM+CN=$\sqrt{2}$;③S△EMN=$\frac{1}{si{n}^{2}α}$,其中正确的是( )
矩形ABCD中,AD=2AB=2$\sqrt{2}$,E是AD的中点,Rt∠FEG顶点与点E重合,将∠FEG绕点E旋转,角的两边分别交AB,BC(或它们的延长线)于点M,N,设∠AME=α(0°<α<90°),有下列结论:①BM=CN;②AM+CN=$\sqrt{2}$;③S△EMN=$\frac{1}{si{n}^{2}α}$,其中正确的是( )| A. | ① | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
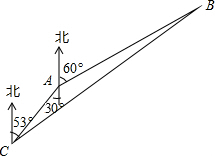 2016年12月底我国首艘航空母舰辽宁舰与数艘去驱航舰组成编队,携多架歼-15舰载战斗机和多型舰载直升机开展跨海区训练和试验任务,在某次演习中,预警直升机A发现在其北偏东60°,距离160千米处有一可疑目标B,预警直升机立即向位于南偏西30°距离40千米处的航母C报告,航母舰载战斗机立即升空沿北偏东53°方向向可疑目标飞去,请求出舰载战斗机到达目标的航程BC.
2016年12月底我国首艘航空母舰辽宁舰与数艘去驱航舰组成编队,携多架歼-15舰载战斗机和多型舰载直升机开展跨海区训练和试验任务,在某次演习中,预警直升机A发现在其北偏东60°,距离160千米处有一可疑目标B,预警直升机立即向位于南偏西30°距离40千米处的航母C报告,航母舰载战斗机立即升空沿北偏东53°方向向可疑目标飞去,请求出舰载战斗机到达目标的航程BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
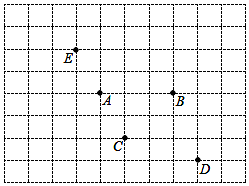 某区进行课堂教学改革,将学生分成5个学习小组,采取团团坐的方式.如图,这是某校七(1)班教室简图,点A、B、C、D、E分别代表五个学习小组的位置,已知C点的坐标为(-2,-2)
某区进行课堂教学改革,将学生分成5个学习小组,采取团团坐的方式.如图,这是某校七(1)班教室简图,点A、B、C、D、E分别代表五个学习小组的位置,已知C点的坐标为(-2,-2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com