
【题目】如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论:
①AD⊥BC;②∠EDA=∠B;③OA= ![]() AC;④DE是⊙O的切线,正确的个数是( )
AC;④DE是⊙O的切线,正确的个数是( )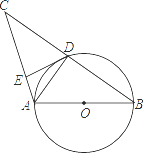
A.1 个
B.2个
C.3 个
D.4个
【答案】D
【解析】解:∵AB是⊙O的直径,
∴∠ADB=90°=∠ADC,
即AD⊥BC,①正确;
连接OD,
∵D为BC中点,
∴BD=DC,
∵OA=OB,
∴DO∥AC,
∵DE⊥AC,
∴OD⊥DE,
∵OD是半径,
∴DE是⊙O的切线,∴④正确;
∴∠ODA+∠EDA=90°,
∵∠ADB=∠ADO+∠ODB=90°,
∴∠EDA=∠ODB,
∵OD=OB,
∴∠B=∠ODB,
∴∠EDA=∠B,∴②正确;
∵D为BC中点,AD⊥BC,
∴AC=AB,
∵OA=OB= ![]() AB,
AB,
∴OA= ![]() AC,∴③正确.
AC,∴③正确.
故答案为:D.
根据直径所对的圆周角是直角可得AD⊥BC;连接OD,根据三角形的中位线定理可得DO∥AC,结合已知条件DE⊥AC可得OD⊥DE,则DE是⊙O的切线;根据DE是⊙O的切线可得∠ODA+∠EDA=90°,而∠ADB=∠ADO+∠ODB=90°可得∠EDA=∠ODB,易得∠EDA=∠B;根据等腰三角形三线合一可得AC=AB,易得OA= ![]() AC。所以选项D符合题意。
AC。所以选项D符合题意。


科目:初中数学 来源: 题型:
【题目】综合与实践
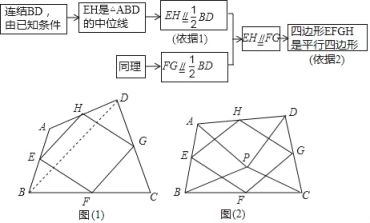
问题情境:在数学活动课上,我们给出如下定义:顺次连按任意一个四边形各边中点所得的四边形叫中点四边形.如图(1),在四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.试说明中点四边形EFGH是平行四边形.
探究展示:勤奋小组的解题思路:
反思交流:
(1)①上述解题思路中的“依据1”、“依据2”分别是什么?
依据1: ;依据2: ;
②连接AC,若AC=BD时,则中点四边形EFGH的形状为 ;
创新小组受到勤奋小组的启发,继续探究:
(2)如图(2),点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并说明理由;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其它条件不变,则中点四边形EFGH的形状为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题: 如图1,在矩形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]() ,点
,点![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,连接所
的中点,连接所![]() 、
、![]() 、
、![]() .
.
求证:![]() 是等边三角形.
是等边三角形.
小明经探究发现,连接![]() 、
、![]() (如图2),从而可证
(如图2),从而可证![]() ,
, ![]() ,使问题得到解决.
,使问题得到解决.

(1)请你按照小明的探究思路,完成他的证明过程;
参考小明思考问题的方法或用其他的方法,解决下面的问题:
(2)如图3,在四边形![]() 中,
中, ![]() ,
,![]() , 对角线
, 对角线![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]() (
(![]() ),点
),点![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,连接
的中点,连接![]() 、
、![]() 、
、![]() .
.
①否存在与![]() 相等的线段?若存在,请找出并证明;若不存在,说明理由.
相等的线段?若存在,请找出并证明;若不存在,说明理由.
②求![]() 的度数.(用含
的度数.(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设![]() ,
, ![]() ,……,
,……, ![]() ,(n为正整数)
,(n为正整数)
(1)试说明![]() 是8的倍数;
是8的倍数;
(2)若△ABC的三条边长分别为![]() 、
、![]() 、
、![]() (
(![]() 为正整数)
为正整数)
①求![]() 的取值范围.
的取值范围.
②是否存在这样的![]() ,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由.
,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OA=90cm,OB=30cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在⊙O的直径BA延长线上,PC与⊙O相切,切点为C,点D在⊙O上,连接PD、BD,已知PC=PD=BC.下列结论:
①PD与⊙O相切;
②四边形PCBD是菱形;
③PO=AB;
④∠PDB=120°.
其中,正确的个数是( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
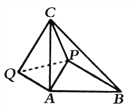
【题目】如图,在等腰ΔABC中,∠CAB=90°AB=AC,P为ΔABC内的一点,且PA=AQ=1,CQ=BP=3,CP=![]() ,求∠APC的大小.(提示:连接PQ)
,求∠APC的大小.(提示:连接PQ)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,分别延长
的中点,分别延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 是矩形;
是矩形;
(2)如图2,连接![]() ,若
,若![]() 平分
平分![]() .
.
①求![]() 的长;
的长;
②如图3,连接![]() ,分别交
,分别交![]() 于点
于点![]() .求证:
.求证:![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.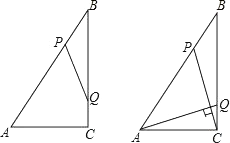
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com