
分析 由根与系数的关系可得x1+x2=-$\frac{3}{2}$、x1•x2=-2,式子$\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}$通分代入可得结论,最后一个式子将其代入x12+x22=(x1+x2)2-2x1•x2中,即可求出结论.
解答 解:∵x1、x2是方程2x2+3x-4=0两个根,
∴x1+x2=-$\frac{3}{2}$,x1x2=-$\frac{4}{2}$=-2,
∴$\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{-\frac{3}{2}}{-2}$=$\frac{3}{4}$,
x12+x22=(x1+x2)2-2x1x2=$(-\frac{3}{2})^{2}$-2×(-2)=$\frac{9}{4}$+4=$\frac{25}{4}$,
故答案为:-$\frac{3}{2}$;-2;$\frac{3}{4}$;$\frac{25}{4}$.
点评 本题考查了根与系数的关系,牢记两根之和等于-$\frac{b}{a}$、两根之积等于$\frac{c}{a}$是解题的关键.


科目:初中数学 来源: 题型:解答题
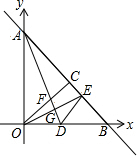 如图,在平面直角坐标系中,直线AB与坐标轴分别交于A、B两点,已知点A的坐标为(0,8),点B的坐标为(8,0),OC、AD均是△OAB的中线,OC、AD相交于点F,OE⊥AD于G交AB于E.
如图,在平面直角坐标系中,直线AB与坐标轴分别交于A、B两点,已知点A的坐标为(0,8),点B的坐标为(8,0),OC、AD均是△OAB的中线,OC、AD相交于点F,OE⊥AD于G交AB于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
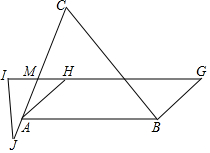 如图所示,已知H为△ABC的垂心,点G满足四边形ABGH为平行四边形.I为直线GH上的点,AC交GI于M.且IM=MH.J为CA延长线上一点,且IJ=AH,求证:I、J、G、C四点共圆.(坐标法不得分)
如图所示,已知H为△ABC的垂心,点G满足四边形ABGH为平行四边形.I为直线GH上的点,AC交GI于M.且IM=MH.J为CA延长线上一点,且IJ=AH,求证:I、J、G、C四点共圆.(坐标法不得分)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{x}^{3}{y}^{2}}{{x}^{2}{y}^{3}}$=$\frac{x}{y}$ | B. | $\frac{a-1}{b-1}$=$\frac{a}{b}$ | C. | $\frac{a-b}{b-a}$=-1 | D. | $\frac{1}{c}$+$\frac{2}{c}$=$\frac{3}{c}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com