
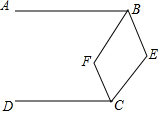
 如图,AB∥CD,E为直线BC右侧一点,连接BE、CE,作∠ABE和∠DCE的角平分线BF、CF相交于点F.
如图,AB∥CD,E为直线BC右侧一点,连接BE、CE,作∠ABE和∠DCE的角平分线BF、CF相交于点F.分析 (1)过E作EG∥AB,根据两直线平行,同旁内角互补,即可得出∠ABE+∠BEC+∠DCE=360°;
(2)过F作FH∥AB,根据两直线平行,内错角相等,即可得出∠BFC=∠ABF+∠DCF;
(3)根据∠ABE和∠DCE的角平分线BF、CF相交于点F,即可得到∠ABE+∠DCE=2(∠ABF+∠DCF),再根据(1)、(2)的结论,可得360°-∠BEC=2∠BFC,进而得到2∠BFC+∠BEC=360°.
解答 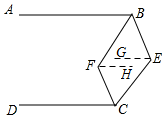 解:(1)如图所示,过E作EG∥AB,
解:(1)如图所示,过E作EG∥AB,
∵AB∥CD,
∴GE∥CD,
∴∠ABE+∠BEG=180°,∠DCE+∠CEG=180°,
∴∠ABE+∠BEG+∠DCE+∠CEG=360°,
∴∠ABE+∠BEC+∠DCE=360°,
即∠ABE+∠DCE=360°-∠BEC;
(2)如图所示,过F作FH∥AB,
∵AB∥CD,
∴FH∥CD,
∴∠ABF=∠BFH,∠DCF=∠CFH,
∴∠BFC=∠BFH+∠CFH=∠ABF+∠DCF,
即∠BFC=∠ABF+∠DCF;
(3)∵∠ABE和∠DCE的角平分线BF、CF相交于点F,
∴∠ABE=2∠ABF,∠DCE=2∠DCF,
∴∠ABE+∠DCE=2(∠ABF+∠DCF),
由(1)、(2)的结论,可得360°-∠BEC=2∠BFC,
∴2∠BFC+∠BEC=360°,
∴当∠BFC=125°时,250°+∠BEC=360°,
∴∠BEC=110°.
点评 此题考查了平行线的性质:两直线平行,同旁内角互补;两直线平行,内错角相等.解题的关键是作出GE和FH这两条辅助线.


科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx-a-b(a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为y=$\frac{8}{9}$x+$\frac{16}{3}$.
如图,抛物线y=ax2+bx-a-b(a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为y=$\frac{8}{9}$x+$\frac{16}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
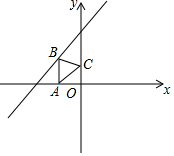 如图,已知点A(-1,0),点B是直线y=x+2上的动点,点C是y轴上的动点,则△ABC的周长的最小值等于( )
如图,已知点A(-1,0),点B是直线y=x+2上的动点,点C是y轴上的动点,则△ABC的周长的最小值等于( )| A. | $\sqrt{10}$ | B. | 2+$\sqrt{2}$ | C. | 1-$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{6}}{3}$ | D. | 1-$\frac{\sqrt{2}+\sqrt{5}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20cm | B. | 24cm | C. | 28cm | D. | 30cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某市为鼓励市民节约用水,自来水公司按分段收费标准收费,如图反映的是每月水费y(元)与用水量x(吨)之间的函数关系.
某市为鼓励市民节约用水,自来水公司按分段收费标准收费,如图反映的是每月水费y(元)与用水量x(吨)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+9=(x+3)2 | B. | a2+4a+4=(a+2)2 | C. | a3-4a=a(a2-4) | D. | 1-4x2=(1+4x)(1-4x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com