
【题目】如图,已知直角坐标系中,A、B、D三点的坐标分别为A(8,0),B(0,4),D(﹣1,0),点C与点B关于x轴对称,连接AB、AC.
(1)求过A、B、D三点的抛物线的解析式;
(2)有一动点E从原点O出发,以每秒2个单位的速度向右运动,过点E作x轴的垂线,交抛物线于点P,交线段CA于点M,连接PA、PB,设点E运动的时间为t(0<t<4)秒,求四边形PBCA的面积S与t的函数关系式,并求出四边形PBCA的最大面积;
(3)抛物线的对称轴上是否存在一点H,使得△ABH是直角三角形?若存在,请直接写出点H的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)S=﹣8t2+32t+32,当t=2时,S有最大值,且最大值为64;(3)H(
;(2)S=﹣8t2+32t+32,当t=2时,S有最大值,且最大值为64;(3)H(![]() ,11),(
,11),(![]() ,
, ![]() ).
).
【解析】试题分析:(1)由于A(8,0),D(﹣1,0),故设过A、B、D三点的抛物线的解析式为y=a(x+1)(x﹣8),将B(0,4)代入即可求得a,进而求得抛物线的解析式为;
(2)四边形PBCA可看作△ABC、△PBA两部分;△ABC的面积是定值,关键是求出△PBA的面积表达式;若设直线l与直线AB的交点为Q,先用t表示出线段PQ的长,而△PAB的面积可由(![]() PQOA)求得,在求出S、t的函数关系式后,由函数的性质可求得S的最大值;
PQOA)求得,在求出S、t的函数关系式后,由函数的性质可求得S的最大值;
(3)根据已知条件得到∠HAB<90°,①当∠ABH=90°时,求得直线AB:y=﹣![]() x+4,直线BH:y=2x+4,于是得到H(
x+4,直线BH:y=2x+4,于是得到H(![]() ,11),②当∠AHB=90°时,过B作BN⊥对称轴于N,则BN=
,11),②当∠AHB=90°时,过B作BN⊥对称轴于N,则BN=![]() ,AG=
,AG=![]() ,设对称轴交x轴于G,根据相似三角形的性质得到HN=
,设对称轴交x轴于G,根据相似三角形的性质得到HN=![]() (负值舍去),于是得到H(
(负值舍去),于是得到H(![]() ,
, ![]() ).
).
(1)∵A(8,0),D(﹣1,0),设过A、B、D三点的抛物线的解析式为y=a(x+1)(x﹣8),将B(0,4)代入得﹣8a=4,∴a=﹣![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() ,即
,即![]() ;
;
(2)△ABC中,AB=AC,AO⊥BC,则OB=OC=4,![]() x+4;依题意,知:OE=2t,即 E(2t,0);∴P(2t,﹣2t2+7t+4)、Q(2t,﹣t+4),PQ=(﹣2t2+7t+4)﹣(﹣t+4)=﹣2t2+8t;S=S△ABC+S△PAB=
x+4;依题意,知:OE=2t,即 E(2t,0);∴P(2t,﹣2t2+7t+4)、Q(2t,﹣t+4),PQ=(﹣2t2+7t+4)﹣(﹣t+4)=﹣2t2+8t;S=S△ABC+S△PAB=![]() ×8×8+
×8×8+![]() ×(﹣2t2+8t)×8=﹣8t2+32t+32=﹣8(t﹣2)2+64;∴当t=2时,S有最大值,且最大值为64;
×(﹣2t2+8t)×8=﹣8t2+32t+32=﹣8(t﹣2)2+64;∴当t=2时,S有最大值,且最大值为64;
(3)存在,∵抛物线的对称轴为:x=![]() =
=![]() ,∵直线x=
,∵直线x=![]() 垂直x轴,∴∠HAB<90°,①当∠ABH=90°时,由A(8,0)、B(0,4),得:直线AB:y=﹣
垂直x轴,∴∠HAB<90°,①当∠ABH=90°时,由A(8,0)、B(0,4),得:直线AB:y=﹣![]() x+4,所以,直线BH可设为:y=2x+h,代入B(0,4),得:h=4,∴直线BH:y=2x+4,当x=
x+4,所以,直线BH可设为:y=2x+h,代入B(0,4),得:h=4,∴直线BH:y=2x+4,当x=![]() 时,y=11,∴H(
时,y=11,∴H(![]() ,11),②当∠AHB=90°时,过B作BN⊥对称轴于N,则BN=
,11),②当∠AHB=90°时,过B作BN⊥对称轴于N,则BN=![]() ,AG=
,AG=![]() ,设对称轴交x轴于G,∵∠AHG=∠HBN=90°﹣∠BHN,∠BNH=∠AGH=90°,∴△AHG∽△BHN,∴
,设对称轴交x轴于G,∵∠AHG=∠HBN=90°﹣∠BHN,∠BNH=∠AGH=90°,∴△AHG∽△BHN,∴![]() ,∴
,∴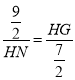 ,∴HN(HN+4)=
,∴HN(HN+4)=![]() ,∴4(HN)2+16HN﹣63=0,解得:HN=
,∴4(HN)2+16HN﹣63=0,解得:HN=![]() (负值舍去),∴H(
(负值舍去),∴H(![]() ,
, ![]() ),综上所述,H(
),综上所述,H(![]() ,11),(
,11),(![]() ,
, ![]() ).
).



科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)若∠DBC=25°,求∠ADC′的度数;
(2)若AB=4,AD=8,求△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE.
填空:① ∠AEB的度数为_______;②线段AD、BE之间的数量关系是______.
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.
(3)探究发现:
图1中的△ACB和△DCE,在△DCE旋转过程中当点A,D,E不在同一直线上时,设直线AD与BE相交于点O,试在备用图中探索∠AOE的度数,直接写出结果,不必说明理由.

【答案】(1)60°.AD=BE;(2)AB=17;(3)∠AOE的度数是60°或120°.
【解析】试题分析:(1)由条件易证△ACD≌△BCE,从而得到:AD=BE,∠ADC=∠BEC.由点A,D,E在同一直线上可求出∠ADC,从而可以求出∠AEB的度数.
(2)仿照(1)中的解法可求出∠AEB的度数,证出AD=BE;由△DCE为等腰直角三角形及CM为△DCE中DE边上的高可得CM=DM=ME,从而证到AE=2CH+BE.
(3)由(1)知△ACD≌△BCE,得∠CAD=∠CBE,由∠CAB=∠ABC=60°,可知∠EAB+∠ABE=120°,根据三角形的内角和定理可知∠AOE=60°.
试题解析:(1)①∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°.
∴∠ACD=∠BCE.
在△ACD和△BCE中,
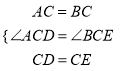 ,
,
∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°.
∴∠BEC=120°.
∴∠AEB=∠BEC∠CED=60°.
故答案为:60°.
②∵△ACD≌△BCE,
∴AD=BE.
故答案为:AD=BE.
(2)∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°.
∴∠ACD=∠BCE.
在△ACD和△BCE中,
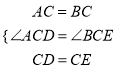 ,
,
∴△ACD≌△BCE(SAS).
∴AD=BE=AE-DE=8,∠ADC=∠BEC,
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°.
∵点A,D,E在同一直线上,
∴∠ADC=135°.
∴∠BEC=135°.
∴∠AEB=∠BEC∠CED=90°.
∴AB=![]() =17;
=17;
(3)由(1)知△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠CAB=∠CBA=60°,
∴∠OAB+∠OBA=120°
∴∠AOE=180°120°=60°,
同理求得∠AOB=60°,
∴∠AOE=120°,
∴∠AOE的度数是60°或120°.
点睛:本题考查了等边三角形的性质、等腰三角形的性质、直角三角形斜边上的中线等于斜边的一半、三角形全等的判定与性质等知识,考查了运用已有的知识和经验解决问题的能力.
【题型】解答题
【结束】
26
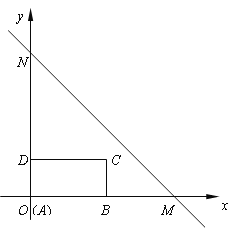
【题目】如图,直线MN:y=-x+b与x轴交于点M(4,0),与y轴交于点N,长方形ABCD的边AB在x轴上,AB=2,AD=1.长方形ABCD由点A与点O重合的位置开始,以每秒1个单位长度的速度沿x轴正方向作匀速直线运动,当点A与点M重合时停止运动.设长方形运动的时间为t秒,长方形ABCD与△OMN重合部分的面积为S.
(1)求直线MN的解析式;
(2)当t=1时,请判断点C是否在直线MN上,并说明理由;
(3)请求出当t为何值时,点D在直线MN上;
(4)直接写出在整个运动过程中S与t的函数关系式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)△ABC的面积为______;
(2)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′,补全△A′B′C′;
(3)若连接AA′,BB′,则这两条线段之间的关系是______;
(4)在图中画出△ABC的高CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
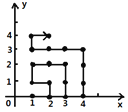
【题目】如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2), (2,2)···根据这个规律,第140个点的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线AB∥CD,点E,F分别在直线AB,CD上,点M为平面内一点.
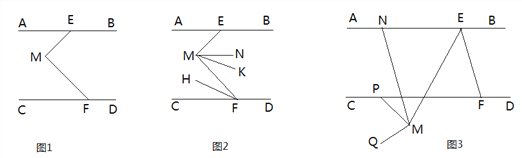
(1)如图1,∠AEM,∠M,∠CFM的数量关系为 ;(直接写出答案)
(2)如图2,∠AEM=48°,MN平分∠EMF,FH平分∠MFC,MK∥FH,求∠NMK的度数;
(3)如图3,点P为CD上一点,∠BEF=n·∠MEF,∠PMQ=n·∠PME,过点M作MN∥EF交AB于点N,请直接写出∠PMQ,∠BEF,∠PMN之间的数量关系.(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
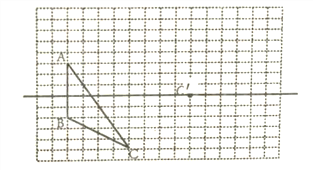
【题目】如图,方格纸中每个小正方形的边长都为l.在方格纸中将三角形ABC经过一次平移后得到三角形A'B'C’,图中标出了点C的对应点C'.
(1)请画出平移后的三角形A'B'C’;
(2)连接AA’,CC’,则这两条线段之间的关系是 ;
(3)建立合适的平面直角坐标系,并写出A'、B'、C'的坐标;
(4)三角形A'B'C'的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com