
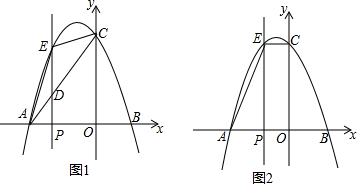
分析 (1)用待定系数法求出抛物线解析式,令x=0求出y轴交点坐标;
(2)先确定出直线AC解析式为y=$\frac{4}{3}$x+8,设出点E的坐标,表示出点D(m,-$\frac{1}{6}$m2+-$\frac{1}{3}$x+4),而点D在直线AC上,列出方程$\frac{4}{3}$m+8=-$\frac{1}{6}$m2+-$\frac{1}{3}$x+4,求出m,从而得出结论;
(3)先求出点P的坐标,再分两种情况计算Ⅰ、当∠AEG=90°时,判断出△EMG∽△APE,得出比例式求解即可,Ⅱ、当∠EAG=90°时,判断出△GNA∽△APE,得到比例式计算.
解答 解:(1)∵点A(-6,0)在抛物线y=-$\frac{1}{3}$x2+bx+8上,
∴0=-$\frac{1}{3}$(-6)2+b(-6)+8,
∴b=-$\frac{2}{3}$,
∴y=-$\frac{1}{3}$x2-$\frac{2}{3}$x+8,
令x=0,y=8,
∴C(0,8)
(2)设E(m,-$\frac{1}{3}$m2-$\frac{2}{3}$m+8),
∴P(m,0),
∵点D为EP中点,
∴DP=DE,D(m,-$\frac{1}{6}$m2+-$\frac{1}{3}$x+4),
∵A(-6,0),C(0,8),
∴直线AC解析式为y=$\frac{4}{3}$x+8,
∵点D在直线AC上,
∴$\frac{4}{3}$m+8=-$\frac{1}{6}$m2+-$\frac{1}{3}$x+4,
∴m=-6(舍)或m=-4,
∴P(-4,0)
∴AP=2,OP=4,
∴$\frac{{S}_{△ADP}}{{S}_{△CDE}}=\frac{\frac{1}{2}DE×AP}{\frac{1}{2}DP×OP}=\frac{AP}{OP}=\frac{1}{2}$;
故答案为1:2
(3)存在点G使得以点A,E,G为顶点的三角形为直角三角形,
连接EG,AG,作GM⊥l,GN⊥x轴,
∵EC∥x轴,
∴EP=CO=8,
把y=8代入y=-$\frac{1}{3}$x2-$\frac{2}{3}$x+8,
∴8=-$\frac{1}{3}$x2-$\frac{2}{3}$x+8,
∴x=0(舍),或x=-2,
∴P(-2,0),
∴AP=AO-PO=4,
Ⅰ、如图1,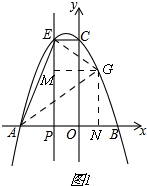
当∠AEG=90°时,
∴∠MEG+∠AEP=90°,
∵∠AEP+∠EAP=90°,
∴∠MEG=∠EAP,
∵∠APE=∠EMG=90°,
∴△EMG∽△APE,
∴$\frac{EM}{AP}=\frac{MG}{EP}$,
设点G(m,-$\frac{1}{3}$m2-$\frac{2}{3}$m+8)(m>0),
∴GN=MP=-$\frac{1}{3}$m2-$\frac{2}{3}$m+8,
∴EM=EP-MP=8-(-$\frac{1}{3}$m2-$\frac{2}{3}$m+8)=y=$\frac{1}{3}$m2+$\frac{2}{3}$m,
MG=PN=PO+ON=2+m,
∵$\frac{EM}{AP}=\frac{MG}{EP}$,
∴$\frac{\frac{1}{3}{m}^{2}+\frac{2}{3}}{4}=\frac{2+m}{8}$,
∴m=-2(舍)或m=$\frac{3}{2}$,
∴G($\frac{3}{2}$,$\frac{25}{4}$);
Ⅱ、如图2,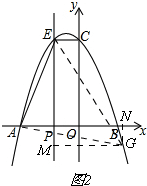
当∠EAG=90°时,
∴∠NAG+∠EAP=90°,
∵∠AEP+∠EAP=90°,
∴∠NAG=∠AEP,
∵∠APE=∠GNA=90°,
∴△GNA∽△APE,
∴$\frac{GN}{AP}=\frac{AN}{EP}$,
设点G(n,-$\frac{1}{3}$n2-$\frac{2}{3}$n+8)(n>0,-$\frac{1}{3}$n2-$\frac{2}{3}$n+8<0),
∴GN=$\frac{1}{3}$m2+$\frac{2}{3}$m+8,
∴AN=AO+ON=6+n,
∵$\frac{GN}{AP}=\frac{AN}{EP}$,
∴$\frac{\frac{1}{3}{n}^{2}+\frac{2}{3}n-8}{4}=\frac{6+n}{8}$,
∴n=-6(舍),或n=$\frac{11}{2}$,
∴G($\frac{11}{2}$,-$\frac{23}{4}$),
符合条件的G点的坐标为G($\frac{3}{2}$,$\frac{25}{4}$)或G($\frac{11}{2}$,-$\frac{23}{4}$),
点评 此题是二次函数综合题,主要考查了待定系数法求函数解析式,相似三角形的性质和判定,判断三角形相似是解本题的关键.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:选择题
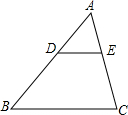 如图,△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,DE=2cm,则BC边的长是( )
如图,△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,DE=2cm,则BC边的长是( )| A. | 6cm | B. | 4cm | C. | 8cm | D. | 7cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 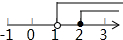 | B. | 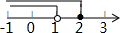 | C. | 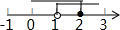 | D. | 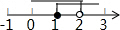 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解全班同学每周体育锻炼的时间 | |
| B. | 鞋厂检查生产鞋底能承受的弯折次数 | |
| C. | 学校招聘新教师,对应聘教师面试 | |
| D. | 某中学调查九年级全体540名学生的平均身高 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com