
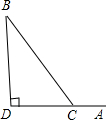
 如图,城市A位于一条铁路线上,而附近的一小镇B需从A市购进大量生活、生产用品,如果铁路运费是公路运费的一半.问该如何从B修筑一条公路到铁路边,使从A到B的运费最低?
如图,城市A位于一条铁路线上,而附近的一小镇B需从A市购进大量生活、生产用品,如果铁路运费是公路运费的一半.问该如何从B修筑一条公路到铁路边,使从A到B的运费最低? 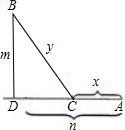 解:设AC=x千米,BC=y千米,AD=n千米,BD=m千米,铁路每千米的运费为a元,则公路每千米的运费为2a元,
解:设AC=x千米,BC=y千米,AD=n千米,BD=m千米,铁路每千米的运费为a元,则公路每千米的运费为2a元,| y2-m2 |
| y2-m2 |
| 3 |
| 3 |
| 3 |
| 3 |
| y2-m2 |
| 3 |
| 3 |
2
| ||
| 3 |
| y2-m2 |
| ||
| 3 |
| ||
| 3 |
| 3 |


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
 如图,半径为30km 的圆A是环保部分划定的生态保护区,B、C是位于保护区附近相距100km的两城市.如果在 B、C两城之间修一条笔直的公路,经测量∠ABC=45°,∠ACB=30°.
如图,半径为30km 的圆A是环保部分划定的生态保护区,B、C是位于保护区附近相距100km的两城市.如果在 B、C两城之间修一条笔直的公路,经测量∠ABC=45°,∠ACB=30°.查看答案和解析>>
科目:初中数学 来源: 题型:
 某市积极响应政府提出的“加快旧城改造,建设新型绿色城市”的号召,将位于居民区较集中的一处破旧厂房进行规划,建成了一个供附近居民休闲散步的公园.在公园的中心建了一个正方形的音乐喷泉(如图).现计划将喷泉四周用花隔开.如有16盆花,要放在喷泉四周,要使每一条边上所放盆花同样多,该怎么放呢?有几种放法?每边放几盆花?试画图说明.
某市积极响应政府提出的“加快旧城改造,建设新型绿色城市”的号召,将位于居民区较集中的一处破旧厂房进行规划,建成了一个供附近居民休闲散步的公园.在公园的中心建了一个正方形的音乐喷泉(如图).现计划将喷泉四周用花隔开.如有16盆花,要放在喷泉四周,要使每一条边上所放盆花同样多,该怎么放呢?有几种放法?每边放几盆花?试画图说明.查看答案和解析>>
科目:初中数学 来源: 题型:
 “中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过25米/秒,如图,一辆汽车在一条城市街路上沿东西方向行驶,某一时刻刚好行驶到距车速检测仪A点距离为40米的C(位于A点北偏东30°处)处,过了3秒钟,到达B点,(位于A点北偏西45°)此时小汽车距车速检测仪间的距离为60米,那么这辆汽车是否超速?
“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过25米/秒,如图,一辆汽车在一条城市街路上沿东西方向行驶,某一时刻刚好行驶到距车速检测仪A点距离为40米的C(位于A点北偏东30°处)处,过了3秒钟,到达B点,(位于A点北偏西45°)此时小汽车距车速检测仪间的距离为60米,那么这辆汽车是否超速?查看答案和解析>>
科目:初中数学 来源:新课标九年级数学竞赛培训第13讲:怎样求最值(解析版) 题型:解答题
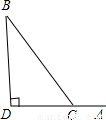
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com