
如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.

科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第4章 基本平面图形 单元测试卷 题型:填空题
已知A、B、C是直线l上的三点,且线段AB=9cm,BC= AB,那么A、C两点的距离是____________.
AB,那么A、C两点的距离是____________.
查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型:解答题
如图,直线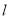 :
:  与
与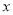 轴、
轴、 轴分别交于点B、C,经过B、C两点的抛物线
轴分别交于点B、C,经过B、C两点的抛物线 与
与 轴的另一个交点为A.
轴的另一个交点为A.
(1)求该抛物线的解析式;
(2)若点P在直线 下方的抛物线上,过点P作PD∥
下方的抛物线上,过点P作PD∥ 轴交
轴交 于点D,PE∥
于点D,PE∥ 轴交
轴交 于点E,
于点E,
求PD+PE的最大值;
(3)设F为直线 上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型:单选题
将二次函数 的图象沿
的图象沿 轴向右平移2个单位长度,得到的函数表达式是( )
轴向右平移2个单位长度,得到的函数表达式是( )
A.  B.
B. 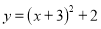 C.
C. 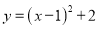 D.
D. 
查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型:单选题
方程 的解为( )
的解为( )
A.  B.
B.  C.
C.  ,
,  D.
D.  ,
, 
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十八章达标检测卷 题型:填空题
如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的关系是S1 S2(填“>”或“<”或“=”)

查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十八章达标检测卷 题型:单选题
下列命题中,真命题是( )
A. 有两边相等的平行四边形是菱形 B. 对角线垂直的四边形是菱形
C. 四个角相等的菱形是正方形 D. 两条对角线相等的四边形是矩形
A 【解析】试题分析:A.反例:等腰梯形;B.反例:风筝型;D.反例:等腰梯形 故选C查看答案和解析>>
科目:初中数学 来源:广西合浦县2017年秋季学期教学质量监测七年级数学试卷 题型:单选题
下面图形不能围成一个长方体的是( )
A. 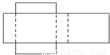
B. 
C. 
D. 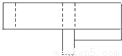
查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型:解答题
用适当的方法解下列方程。
(1)3x(x+3)=2(x+3)
(2)2x2?4x?3=0.
(1)x1=?3,x2= (2) 【解析】试题分析:第小题用因式分解法,第小题用公式法. 试题解析::(1)3x(x+3)-2(x+3)=0, (x+3)(3x-2)=0, 或 (2) ∴ ∴x1=1+,x2=1-.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com