
����Ŀ����ͼ����ƽ��ֱ�������У���OΪ����ԭ�㣬ֱ��y=��x+4��x�ύ�ڵ�A������A��������y=ax2+bx��ֱ��y=��x+4������һ��B���ҵ�B�ĺ�����Ϊ1��
��1����a��b��ֵ��
��2����P���߶�AB��һ���㣨��P�����A��B�غϣ�������P��PM��OB����һ�����ڵ��������ڵ�M������M��MC��x���ڵ�C����AB�ڵ�N������P��PF��MC�ڵ�F����PF�ij�Ϊt��MN�ij�Ϊd����d��t֮��ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
��3���ڣ�2���������£���S��ACN=S��PMNʱ������ON����Q���߶�BP�ϣ�����Q��QR��MN��ON�ڵ�R������MQ��BR������MQR����BRN=45��ʱ�����R�����꣮
���𰸡�
��1���⣺��y=��x+4��x�ύ�ڵ�A��
��A��4��0����
�ߵ�B�ĺ�����Ϊ1����ֱ��y=��x+4������B��
��B��1��3����
��������y=ax2+bx����A��4��0����B��1��3����
�� ![]() ��
��
��ã� ![]() ��
��
��a=��1��b=4��
��2���⣺����һ��
��ͼ����BD��x���ڵ�D���ӳ�MP��x���ڵ�E��
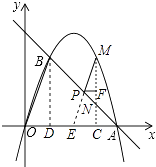
��B��1��3����A��4��0����
��OD=1��BD=3��OA=4��
��AD=3��
��AD=BD��
�ߡ�BDA=90�㣬��BAD=��ABD=45�㣬
��MC��x�ᣬ���ANC=��BAD=45�㣬
���PNF=��ANC=45�㣬
��PF��MC��
���FPN=��PNF=45�㣬
��NF=PF=t��
�ߡ�PFM=��ECM=90�㣬
��PF��EC��
���MPF=��MEC��
��ME��OB�����MEC=��BOD��
���MPF=��BOD��
��tan��BOD=tan��MPF��
�� ![]() =
= ![]() =3��
=3��
��MF=3PF=3t��
��MN=MF+FN��
��d=3t+t=4t��
��������
�ӳ�MP��x���ڵ�M�䣬��M��N���MN��AB��N�䣬
�ӳ�FP��M��N����F�䣬��M��N���MN�����PMN�ס�PM��N�䣬
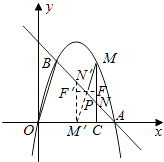
�� ![]() ����O��0��0����B��1��3����
����O��0��0����B��1��3����
��KOB=3��
��PM��OB��
��KPM=KOB=3����lPM��y=3x+b����P��p����p+4������b=4��4p��
��lPM��y=3x+4��4P����y=0���룬��x= ![]() ��
��
��M�䣨 ![]() ��0����
��0����
��N��x=M��x����x= ![]() ����y=��x+4��
����y=��x+4��
��y= ![]() ��
��
��N�䣨 ![]() ��
�� ![]() ������M��N��=
������M��N��= ![]() ��
��
��PF���M��N�䣬
��PF��=p�� ![]() =
= ![]() ��
��
�� ![]() ��
��
��3���⣺����һ��
�籸��ͼ���ɣ�2��֪��PF=t��MN=4t��

��S��PMN= ![]() MN��PF=
MN��PF= ![]() ��4t��t=2t2��
��4t��t=2t2��
�ߡ�CAN=��ANC��
��CN=AC��
��S��ACN= ![]() AC2��
AC2��
��S��ACN=S��PMN��
�� ![]() AC2=2t2��
AC2=2t2��
��AC=2t��
��CN=2t��
��MC=MN+CN=6t��
��OC=OA��AC=4��2t��
��M��4��2t��6t����
�ɣ�1��֪�����ߵĽ���ʽΪ��y=��x2+4x��
��M��4��2t��6t������y=��x2+4x�ã�
����4��2t��2+4��4��2t��=6t��
��ã�t1=0���ᣩ��t2= ![]() ��
��
��PF=NF= ![]() ��AC=CN=1��OC=3��MF=
��AC=CN=1��OC=3��MF= ![]() ��PN=
��PN= ![]() ��PM=
��PM= ![]() ��AN=
��AN= ![]() ��
��
��AB=3 ![]() ��
��
��BN=2 ![]() ��
��
��NH��RQ�ڵ�H��
��QR��MN��
���MNH=��RHN=90�㣬��RQN=��QNM=45�㣬
���MNH=��NCO��
��NH��OC��
���HNR=��NOC��
��tan��HNR=tan��NOC��
�� ![]() =
= ![]() =
= ![]() ��
��
��RH=n����HN=3n��
��RN= ![]() n��QN=3
n��QN=3 ![]() n��
n��
��PQ=QN��PN=3 ![]() n��
n�� ![]() ��
��
��ON= ![]() =
= ![]() ��
��
OB= ![]() =
= ![]() ��
��
��OB=ON�����OBN=��BNO��
��PM��OB��
���OBN=��MPB��
���MPB=��BNO��
�ߡ�MQR����BRN=45�㣬��MQR=��MQP+��RQN=��MQP+45�㣬
���BRN=��MQP��
���PMQ�ס�NBR��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��ã�n= ![]() ��
��
��R�ĺ�����Ϊ��3�� ![]() =
= ![]() ��R����������1��
��R����������1�� ![]() =
= ![]() ��
��
��R�� ![]() ��
�� ![]() ����
����
��������
��M��t����t2+4t����N��t����t+4����
��MN=��t2+4t+t��4=��t2+5t��4��
��PF= ![]() ����t2+5t��4����
����t2+5t��4����
��S��PMN= ![]() ����t2+5t��4��2=
����t2+5t��4��2= ![]() ��t��4��2��t��1��2��
��t��4��2��t��1��2��
��KAB=��1�����OAB=45�㣬
��CA=CN=4��t��
��S��ACN= ![]() ��t��4��2��
��t��4��2��
��S��ACN=S��PMN��
�� ![]() ��t��4��2��t��1��2=
��t��4��2��t��1��2= ![]() ��t��4��2��
��t��4��2��
��t1=��1�����ᣩ��t2=3��
��M��3��3����
��MX=NX=3��
��N��3��1����
��ON= ![]() ��
��
��B��1��3����
��OB= ![]() ��
��
��OB=ON����OBN=��ONB��
��OB��MP
���OBN=��QPM��
���ONB=��QPM����RQA=45�㣬
�ߡ�MQR����BRN=45�㣬
���BRN=��MQP��
���BRN�ס�MQP��
�� ![]() ��
��
��KPM=3��M��3��3����
��lPM��y=3x��6��
��lAB��y=��x+4��
��P��2.5��1.5����
��R��3t��t����
��Q��3t����3t+4����
�� ![]() ��
��
��t1= ![]() ��t2=
��t2= ![]() ���ᣩ��
���ᣩ��
��R�� ![]() ��
�� ![]() ����
����
������������ֱ�߽���ʽ���A��B���꣬���������߽���ʽ�������a��b����2������ƽ���ߵ����ʿ��Ƴ���MPF=��BOD��tan��BOD=tan��MPF����t�Ĵ���ʽ��ʾ�߶Σ��������ж���ʽ�У��ó���ϵʽ����3������֪��MQR����BRN=45�㣬���ƽ�����ʣ��ɵá�BRN=��MQP������֤����BRN�ס�MQP����Ӧ�߳ɱ��������г�����t�ķ��̣����R����.


 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
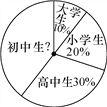
����Ŀ��ij��ѧ������Ӫ�����Сѧ�������������������ʹ�ѧ���μӣ���200�ˣ�����ѧ����������������ͳ��ͼ��
(1)�μ��������Ӫ��ij��������ж����ˣ�
(2)���֯�ߺ��ٲμ��������Ӫ�������ѧ��Ϊƶ��ѧ�������Сѧ��ÿ��
��� 5 Ԫ��������ÿ�˾�� 10 Ԫ��������ÿ�˾�� 15 Ԫ����ѧ��ÿ�˾�� 20 Ԫ����ƽ�� ÿ�˾���Ƕ���Ԫ��
(3)��(2)�������£���ÿ��ѧ���ľ������(��ԪΪ��λ)������¼�������������������У������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C��90�㣬��A��30�㣬AB�Ĵ�ֱƽ���߽�AC�ڵ�D����AB�ڵ�E��CD��2����AC����( )
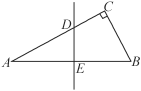
A. 4 B. 5 C. 6 D. 8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ�ٰ조�������Ļ��С��Ϊ�˴λ�����һ��������ɽΪ������ͼ�꣨��ͼ�������ú졢��������ɫ��ͼ���е�A��B��C��������������ֱ�Ϳɫ��һ������ֻͿһ����ɫ��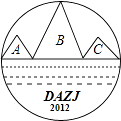
��1��������״ͼ�г�����Ϳɫ�Ŀ��ܽ����
��2������������������������Ϳ��ɫ�ǡ������ɫ��һ���ɫ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�١��ڡ��ۣ���������ABC��������ABCD���������ABCDE�ֱ��ǡ�O���ڽ������Ρ��ڽ��ı��Ρ��ڽ�����Σ���M��N�ֱ�ӵ�B��C��ʼ������ͬ���ٶ��С�O����ʱ���˶���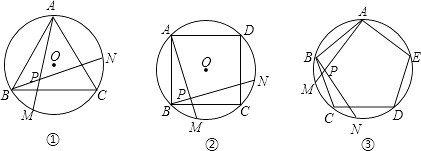
��1����ͼ���С�APB�Ķ�����
��2��ͼ���У���APB�Ķ����� �� ͼ���С�APB�Ķ�������
��3������ǰ��̽�������ܷ����ƹ㵽һ�����n������������ܣ�д���ƹ�����ͽ��ۣ������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ȼ��![]() �ĸ�λ���ֱ�Ϊ0��1��2������9ʱ��
�ĸ�λ���ֱ�Ϊ0��1��2������9ʱ��![]() �ĸ�λ�������ʾ��
�ĸ�λ�������ʾ��
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 |
| 0 | 1 | 8 | 7 | 4 | 5 | 6 | 3 | 2 | 9 |
| 0 | 1 | 6 | 1 | 6 | 5 | 6 | 1 | 6 | 1 |
������������ |
��10��11��12��13���ĸ����У���![]() ____________ʱ������
____________ʱ������![]() �ܱ�5������
�ܱ�5������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڲ�Ա�����ཻ��ְλ�ǹ�˾�������˵�һ��ģʽ����ͼ1��λ�ڳɶ���ij�����ܹ�˾�ھ���ɶ�![]() ��
��![]() ������һ���ֹ�˾���ֶ�����ְ1����ܹ�˾Сӱ�ͷֹ�˾С����ְλ����ѧϰ����������Сӱ�����ӳɶ�������1��Сʱ��С��������
������һ���ֹ�˾���ֶ�����ְ1����ܹ�˾Сӱ�ͷֹ�˾С����ְλ����ѧϰ����������Сӱ�����ӳɶ�������1��Сʱ��С��������![]() �г��������Ը��Ե��ٶ�������ʻ��С��������;��
�г��������Ը��Ե��ٶ�������ʻ��С��������;��![]() ��ʱͻȻ�ӵ��ֹ�˾����ֻ֪ͨ��ԭ·ԭ�ٷ��أ���Сӱ����һֱ�ӳɶ�ֱ��
��ʱͻȻ�ӵ��ֹ�˾����ֻ֪ͨ��ԭ·ԭ�ٷ��أ���Сӱ����һֱ�ӳɶ�ֱ��![]() �У��������ͬʱ����
�У��������ͬʱ����![]() �У�Сӱ��С������Գ����ص�·��
�У�Сӱ��С������Գ����ص�·��![]() (ǧ��)��С�������������õ�ʱ��
(ǧ��)��С�������������õ�ʱ��![]() (Сʱ)�Ĺ�ϵ��ͼ2�����ͼ����Ϣ����������⣺
(Сʱ)�Ĺ�ϵ��ͼ2�����ͼ����Ϣ����������⣺
��1��Сӱ���ٶ���____________ǧ��/ʱ��ͼ2��![]() ____________��С�����ٶ���____________ǧ��/ʱ��
____________��С�����ٶ���____________ǧ��/ʱ��
��2����д��С�������ij�����![]() �еľ���
�еľ���![]() ����������ʱ��
����������ʱ��![]() �Ĺ�ϵʽ��
�Ĺ�ϵʽ��
��3��ֱ��д��Сӱ��С�����100ǧ��ʱ![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ǿѧ�����������ijУ��չ��������μ䡱���ѧУ������ѧ���п���A������B��������Զ��C��������D���ܲ���E���������ֻ��Ŀ��Ϊ���˽�ѧ����������Ŀ��ϲ������������ȡ�˲���ѧ�����е��飬�������������Ƴ���ͼ��ʾ������ͳ��ͼ������ͼ�е���Ϣ����������⣺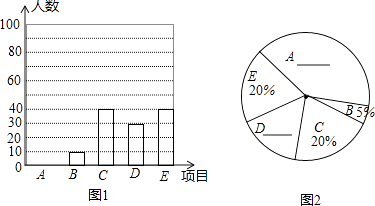
��1������������У�����������ѧ����
��2���뽫����ͳ��ͼ����������
��3������У��1200����Уѧ���������ϲ�������ѧ����Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪������һ��ͼ�Σ�ͨ����ͬ�ķ�������ͼ�ε�������Եõ�һ����ѧ��ʽ.���磺��ͼ1�ɵõ�![]() .
.

��1��д����ͼ2����ʾ����ѧ��ʽ��________.

��2��д����ͼ3����ʾ����ѧ��ʽ��________.

��3����֪ʵ��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() .
.
����![]() ��ֵ.
��ֵ.
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com