
【题目】在一个不透明的口袋里装有分别标有数字﹣3、﹣1、0、2的四个小球,除数字不同外,小球没有任何区别,每次实验先搅拌均匀.
(1)从中任取一球,求抽取的数字为正数的概率;
(2)从中任取一球,将球上的数字记为a,求关于x的一元二次方程ax2﹣2ax+a+3=0有实数根的概率;
(3)从中任取一球,将球上的数字作为点的横坐标,记为x(不放回);再任取一球,将球上的数字作为点的纵坐标,记为y,试用画树状图(或列表法)表示出点(x,y)所有可能出现的结果,并求点(x,y)落在第二象限内的概率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)四个数字中正数有一个,求出所求概率即可;
(2)表示出已知方程根的判别式,根据方程有实数根求出a的范围,即可求出所求概率;
(3)列表得出所有等可能的情况数,找出点(x,y)落在第二象限内的情况数,即可求出所求的概率.
试题解析:解:(1)根据题意得:抽取的数字为正数的情况有1个,则P=![]() ;
;
(2)∵方程ax2﹣2ax+a+3=0有实数根,
∴△=4a2﹣4a(a+3)=﹣12a≥0,且a≠0,
解得:a<0,
则关于x的一元二次方程ax2﹣2ax+a+3=0有实数根的概率为![]() ;
;
(3)列表如下:
﹣3 | ﹣1 | 0 | 2 | |
﹣3 | ﹣﹣﹣ | (﹣1,﹣3) | (0,﹣3) | (2,﹣3) |
﹣1 | (﹣3,﹣1) | ﹣﹣﹣ | (0,﹣1) | (2,﹣1) |
0 | (﹣3,0) | (﹣1,0) | ﹣﹣﹣ | (2,0) |
2 | (﹣3, | (﹣1,2) | (0,2) | ﹣﹣﹣ |
所有等可能的情况有12种,其中点(x,y)落在第二象限内的情况有2种,
则P=![]() =
=![]() .
.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
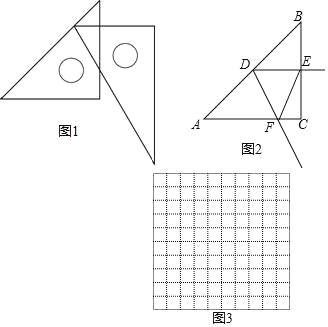
【题目】在数学活动课上,老师提出了一个问题:把一副三角尺如图1摆放,直角三角尺的两条直角边分别垂直或平行,60°角的顶点在另一个三角尺的斜边上移动,在这个运动过程中,有哪些变量,能研究它们之间的关系吗?
小林选择了其中一对变量,根据学习函数的经验,对它们之间的关系进行了探究.下面是小林的探究过程,请补充完整:
(1)画出几何图形,明确条件和探究对象;
如图2,在Rt△ABC中,∠C=90°,AC=BC=6cm,D是线段AB上一动点,射线DE⊥BC于点E,∠EDF=_____°,射线DF与射线AC交于点F.设B,E两点间的距离为xcm,E,F两点间的距离为ycm.
(2)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 6.9 | 5.3 | 4.0 | 3.3 | ____ | 4.5 | 6 |
(说明:补全表格时相关数据保留一位小数)
(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(4)结合画出的函数图象,解决问题:当△DEF为等边三角形时,BE的长度约为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
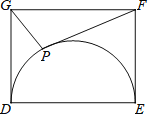
【题目】在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )
A. ![]() B.
B. ![]() C. 34 D. 10
C. 34 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为 .
问题探究
(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
问题解决
(3)如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在![]() 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).
、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).



图① 图② 图③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ACB与∠CAB的平分线交于点P,PD⊥AB于点D,若△APC与△APD的周长差为![]() ,四边形BCPD的周长为12+
,四边形BCPD的周长为12+![]() ,则BC等于______.
,则BC等于______.

查看答案和解析>>
科目:初中数学 来源: 题型:
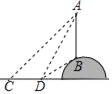
【题目】如图,为了测量小山顶的铁塔AB高度,王华和杨丽在平地上的C点处测得A点的仰角为45°,向前走了18m后到达D点,测得A点的仰角为60°,B点的仰角为30°
(1)求证:AB=BD;
(2)求证铁塔AB的高度.(结果精确到0.1米,其中![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
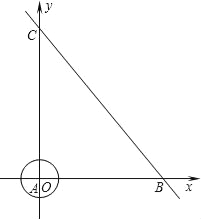
【题目】如图,在直角坐标系中,半径为1的⊙A圆心与原点O重合,直线l分别交x轴、y轴于点B、C,点B的坐标为(6,0),∠ABC=60°.
(1)若点P是⊙A上的动点,则P到直线BC的最小距离是 .
(2)若点A从原点O出发,以1个单位/秒的速度沿着线路OB→BC→CO运动,回到点O停止运动,⊙A随着点A的运动而移动.设点A运动的时间为t.
①求⊙A在整个运动过程中与坐标轴相切时t的取值;
②求⊙A在整个运动过程中所扫过的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
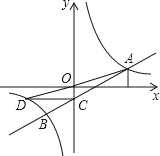
【题目】如图,一次函数y=ax+b与反比例函数y=![]() 的图象交于A、B两点,点A坐标为(m,2),点B坐标为(﹣4,n),OA与x轴正半轴夹角的正切值为
的图象交于A、B两点,点A坐标为(m,2),点B坐标为(﹣4,n),OA与x轴正半轴夹角的正切值为![]() ,直线AB交y轴于点C,过C作y轴的垂线,交反比例函数图象于点D,连接OD、BD.
,直线AB交y轴于点C,过C作y轴的垂线,交反比例函数图象于点D,连接OD、BD.
(1)求一次函数与反比例函数的解析式;
(2)求四边形OCBD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com