
【题目】已知菱形ABCD在平面直角坐标系的位置如图所示,A(1,1),B(6,1),AC=4 ![]() ,点P是对角线OAC上的一个动点,E(0,2),当△EPD周长最小时,点P的坐标为( )
,点P是对角线OAC上的一个动点,E(0,2),当△EPD周长最小时,点P的坐标为( ) 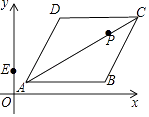
A.(2,2)
B.(2, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
【答案】D
【解析】解:连接ED,如图, 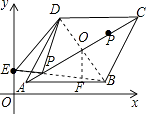
∵点D关于AC的对称点是点B,
∴DP=BP,
∴EB即为EP+DP最短,
即此时△EPD周长最小,
连接BD交AC于O,
过O作OF⊥AB于F,
∵四边形ABCD是菱形,
∴AO= ![]() AC=2
AC=2 ![]() ,AC⊥BD,
,AC⊥BD,
∴BO= ![]() =
= ![]() ,
,
∴OF= ![]() =2,
=2,
∴AF= ![]() =4,
=4,
∵A(1,1),B(6,1),
∴AB∥x轴,
∴直线AB与x轴间的距离是1,
∴O点的纵坐标为2+1=3,
∴O(5,3),
∴直线AC的解析式为:y= ![]() x+
x+ ![]() ,
,
∵E(0,2),B(6,1),
∴直线BE的解析式为:y=﹣ ![]() x+2,
x+2,
解 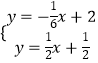 得:
得: 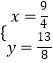 ,
,
∴P( ![]() ,
, ![]() ).
).
故选D.
【考点精析】解答此题的关键在于理解菱形的性质的相关知识,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.


科目:初中数学 来源: 题型:
【题目】我市进行运河带绿化,计划种植银杏树苗,现甲、乙两家有相同的银杏树苗可供选择,其具体销售方案如下:
甲:购买树苗数量不超过500棵时,销售单价为800元![]() 棵;超过500棵的部分,销售单价为700元
棵;超过500棵的部分,销售单价为700元![]() 棵.
棵.
乙:购买树苗数量不超过1000棵时,销售单价为800元![]() 棵;超过1000棵的部分,销售单价为600元
棵;超过1000棵的部分,销售单价为600元![]() 棵.
棵.
设购买银杏树苗x棵,到两家购买所需费用分别为![]() 元、
元、![]() 元
元![]()
(1)该景区需要购买800棵银杏树苗,若都在甲家购买所要费用为______元,若都在乙家购买所需费用为______元;
(2)当![]() 时,分别求出
时,分别求出![]() 、
、![]() 与x之间的函数关系式;
与x之间的函数关系式;
(3)如果你是该景区的负责人,购买树苗时有什么方案,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数的图象经过点A(2,3)与点B(0,5).
(1)求此一次函数的表达式;
(2)若点P为此一次函数图象上一点,且△POB的面积为10,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A∶∠B∶∠C=3∶5∶10,又△MNC≌△ABC,则∠BCM∶∠BCN等于( )

A. 1∶2 B. 1∶3 C. 2∶3 D. 1∶4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。
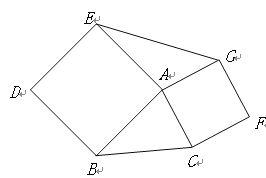
(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= ![]() 的图象上运动,tan∠CAB=2,则关于x的方程x2﹣5x+k=0的解为 .
的图象上运动,tan∠CAB=2,则关于x的方程x2﹣5x+k=0的解为 . 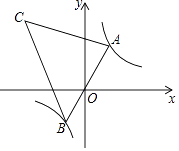
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠DOC为直角,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论错误的是( )
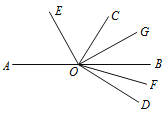
A. ∠DOG与∠BOE互补 B. ∠AOE-∠DOF=45°
C. ∠EOD与∠COG互补 D. ∠AOE与∠DOF互余
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,F是AD的中点,延长BC到点E,使CE=
ABCD中,F是AD的中点,延长BC到点E,使CE=![]() BC,连结DE,CF。
BC,连结DE,CF。

(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中 ![]() 的长是cm(计算结果保留π).
的长是cm(计算结果保留π).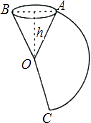
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com