
 在平面直角坐标系xOy中,△ABC的位置如图所示,先把△ABC沿x轴翻折,再把所得图形沿y轴翻折,得到△A1B1C1.
在平面直角坐标系xOy中,△ABC的位置如图所示,先把△ABC沿x轴翻折,再把所得图形沿y轴翻折,得到△A1B1C1.分析 (1)根据轴对称的性质画出图形,再由△ABC和△A1B1C1在坐标系中的位置指出其位置关系即可;
(2)连接OA,OC,设点O到直线AC的距离为h,根据勾股定理求出AC的长,再由三角形的面积即可得出h的长,即为该圆的半径长.
解答 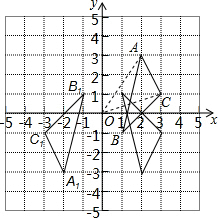 解:(1)如图所示,由图可知,△ABC和△A1B1C1关于原点对称;
解:(1)如图所示,由图可知,△ABC和△A1B1C1关于原点对称;
(2)连接OA,OC,设点O到直线AC的距离为h,
∵AC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴S△OAC=$\frac{1}{2}$×$\sqrt{5}$•h=3×3-$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×2×3=$\frac{7}{2}$,
∴h=$\frac{7\sqrt{5}}{5}$.
∴该圆的半径长为:$\frac{7\sqrt{5}}{5}$.
故答案为:$\frac{7\sqrt{5}}{5}$.
点评 此题主要考查了平移变换和轴对称变换以及切线的性质、三角形面积求法,根据题意得出对应点位置是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图:已知AB⊥DB于B点,CD⊥DB于D点,AB=6,CD=4,BD=14,在DB上取一点P,使以CDP为顶点的三角形与以PBA为顶点的三角形相似,则DP的长.
如图:已知AB⊥DB于B点,CD⊥DB于D点,AB=6,CD=4,BD=14,在DB上取一点P,使以CDP为顶点的三角形与以PBA为顶点的三角形相似,则DP的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -5 | B. | 0.1 | C. | $\frac{4}{7}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com