
 如图,△ABC中,AB=AC,△DEF是△ABC的内接正三角形,则下列关系式成立的是( )
如图,△ABC中,AB=AC,△DEF是△ABC的内接正三角形,则下列关系式成立的是( )| A. | 2∠1=∠2+∠3 | B. | 2∠2=∠1+∠3 | C. | 2∠3=∠1+∠2 | D. | ∠1+∠2+∠3=90° |
分析 先根据等腰三角形的性质及三角形内角和定理可知∠A+2∠B=180°,由△DEF是等边三角形可知∠AEF=120°-∠2,∠BFD=120°-∠3,由三角形内角和定理可知∠A+∠AFD+∠3=180°,∠B+∠1+∠BDE=180°,再把所得式子联立即可求出∠1、∠2、∠3的关系.
解答  解:∵△ABC中,AB=AC,
解:∵△ABC中,AB=AC,
∴∠B=∠C,
∴∠A+2∠B=180°①,
∵△DEF是等边三角形,
∴∠AFD=120°-∠2,∠BDE=120°-∠3,
在△ADF中,∠A+∠AFD+∠3=180°,即∠A+120°-∠2+∠3=180°②,
在△BDE中,∠B+∠1+∠BDE=180°,即∠B+∠2+120°-∠3=180°③,
①②③联立,解得∠1=$\frac{∠2+∠3}{2}$.
则2∠1=∠2+∠3.
故选:A.
点评 本题考查的是等边三角形及等腰三角形的性质,解答此类题目时往往用到三角形的内角和是180°是解答此题的关键.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
 如图,四边形的两条对角线AC、BD所成的锐角为45°,当AC+BD=18时,四边形ABCD的面积最大值是( )
如图,四边形的两条对角线AC、BD所成的锐角为45°,当AC+BD=18时,四边形ABCD的面积最大值是( )| A. | $\frac{75}{4}$$\sqrt{2}$ | B. | 19$\sqrt{2}$ | C. | $\frac{81}{4}$$\sqrt{2}$ | D. | 21$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
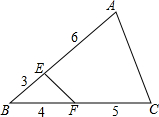 如图,三角形ABC被分成三角形BEF和四边形AEFC两部分,BE=3,BF=4,FC=5,AE=6,那么三角形BEF面积和四边形AEFC面积的比是( )
如图,三角形ABC被分成三角形BEF和四边形AEFC两部分,BE=3,BF=4,FC=5,AE=6,那么三角形BEF面积和四边形AEFC面积的比是( )| A. | 4:23 | B. | 4:25 | C. | 5:26 | D. | 1:6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+3)(x-4) | B. | (x-3)(x+4) | C. | 2(x+3)(x-4) | D. | 2(x-3)(x+4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com