练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．如图，将一张正方形纸片按图①，图②所示方法折叠，得到图③，再将图③按虚线剪裁得到图④，将图④展开后得到的图案是（　　）
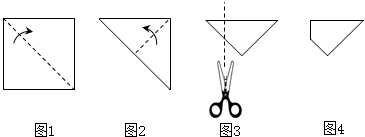
    A．B．C．D．

    分析 对于此类问题，学生只要亲自动手操作，答案就会很直观地呈现．

    解答 解：严格按照图中的顺序向右上翻折，向左上角翻折，剪去左上角，展开得到结论．
    故选：B．

    点评 本题考查的是剪纸问题，此类题目主要考查学生的动手能力及空间想象能力，对于此类问题，学生只要亲自动手操作，答案就会很直观地呈现．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016~2017学年安徽省芜湖市九年级下学期第一次模拟考试数学试卷（解析版） 题型：选择题

    如图，直线l和双曲线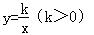交于A、B两点，P是线段AB上的点（不与A、B重合），过点A、B、P分别向x轴作垂线，垂足分别为C、D、E，连接OA、OB、0P，设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3，则（　　）

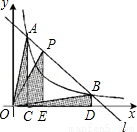
    A．S1＜S2＜S3B．S1＞S2＞S3C．S1=S2＞S3D．S1=S2＜S3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

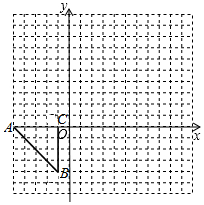    8．如图，直角坐标系中的△ABC的三个顶点分别为A（-5，0），B（-1，-4），C（-1，0）．
    （1）直接写出AB的中点M关于y轴的对称点M′的坐标；
    （2）画出△ABC关于点O的中心对称图形△A′B′C′；
    （3）以点C′为旋转中心，将点M′逆时针旋转，旋转角为α（0°＜α＜180°），直接写出使点M′落在△A′B′C′内部时a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，在Rt△ABC中，∠A=90°，AB=AC=4，将△ABC折叠，使点B落在边AC上的D处，折痕为PQ．
    （1）当点D与点A重合时，折痕PQ的长为2；
    （2）设AD=x，AP=y．
    ①求y与x的函数表达式，并写出自变量x的取值范围；
    ②当x取何值时，重叠部分为等腰三角形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．在正方形ABCD中，点P在射线AB上，连结PC，PD，M，N分别为AB，PC中点，连结MN交PD于点Q．
    （1）如图1，当点P与点B重合时，求∠QMB的度数；
    （2）当点P在线段AB的延长线上时．
    ①依题意补全图2
    ②小聪通过观察、实验、提出猜想：在点P运动过程中，始终有QP=QM．
    小聪把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：
    想法1延长BA到点E，使AE=PB．要证QP=QM，只需证△PDA≌△ECB．
    想法2：取PD中点E，连结NE，EA．要证QP=QM只需证四边形NEAM是平行四边形．
    想 法3：过N作NE∥CB交PB于点E，要证QP=QM，只要证明△NEM∽△DAP．
    …
    请你参考上面的想法，帮助小聪证明QP=QM．（一种方法即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．一个盒子中装有2个白球，5个红球，从这个盒子中随机摸出一个球，是红球的概率为$\frac{5}{7}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

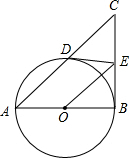    9．如图，AB为⊙O的直径，E是⊙O外一点，过点E作⊙O的两条切线ED、EB，切点分别为点D，B，连接AD并延长交BE延长线于点C，连接OE．
    （1）试判断OE与AC的关系，并说明理由；
    （2）填空：
    ①当∠BAC=45°时，四边形ODEB是正方形．
    ②当∠BAC=30°时，$\frac{AD}{DE}$的值为4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．如图，直线a∥b，将一个直角三角尺按如图所示的位置摆放，若∠1=58°，则∠2的度数为（　　）
    A．30°B．32°C．42°D．58°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．据调查，超速行驶是引发交通事故的主要原因之一，所以规定以下情境中的速度不得超过15m/s，在一条笔直公路BD的上方A处有一探测仪．如图，AD=24m，∠D=90°，第一次探测到一辆轿车从B点匀速向D点行驶，测得∠ABD=31°，2秒后到达C点，测得∠ACD=50°
    （1）求B，C的距离．  
    （2）通过计算，判断此轿车是否超速．（tan31°≈0.6，tan50°≈1.2，结果精确到1m）

    查看答案和解析>>

    同步练习册答案