

 ,求出所用的时间;当6≤t≤16时,点P与C重合,即
,求出所用的时间;当6≤t≤16时,点P与C重合,即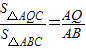 ,根据△AQC的面积恰好为△ABC面积一半,求出所用的时间.
,根据△AQC的面积恰好为△ABC面积一半,求出所用的时间. .
. ,
,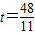 (2分)
(2分)
 ,
,
 ,
,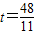 时,△AQP∽△ABC
时,△AQP∽△ABC ∴PD=APsin∠A,CE=ACsin∠A.
∴PD=APsin∠A,CE=ACsin∠A. ,
, ,
, ,
,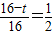 ,
,

科目:初中数学 来源:2009年上海市普陀区中考数学一模试卷(解析版) 题型:解答题
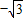 ,1).
,1).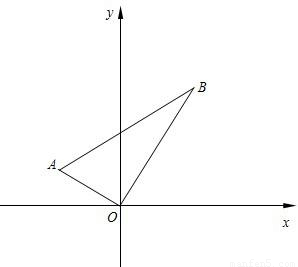
查看答案和解析>>
科目:初中数学 来源:2009年上海市普陀区中考数学一模试卷(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2009年上海市普陀区中考数学一模试卷(解析版) 题型:解答题
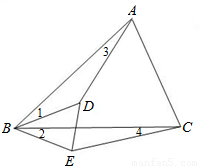
查看答案和解析>>
科目:初中数学 来源:2009年上海市普陀区中考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com