
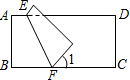
 如图,把长方形纸片ABCD沿EF对折,若∠1=40°,则∠AEF=110°.
如图,把长方形纸片ABCD沿EF对折,若∠1=40°,则∠AEF=110°.  手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:解答题
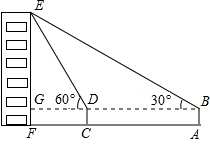 如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)
如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
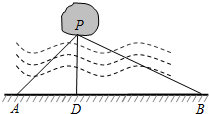 如图,湖中有一小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,在小道上测得如下数据:AB=60米,∠PAB=45°,∠PBA=30°.请求出小桥PD的长.
如图,湖中有一小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,在小道上测得如下数据:AB=60米,∠PAB=45°,∠PBA=30°.请求出小桥PD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{1}{2}$x+1 | B. | y=$\frac{1}{2}$x-1 | C. | y=-$\frac{1}{2}$x-1 | D. | y=-$\frac{1}{2}$x+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com