
【题目】某公司技术人员用“沿直线AB折叠检验塑胶带两条边缘线a、b是否互相平行”.
(1)如图1,测得∠1=∠2,可判定a∥b吗?请说明理由;
(2)如图2,测得∠1=∠2,且∠3=∠4,可判定a∥b吗?请说明理由;
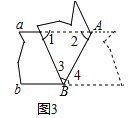
(3)如图3,若要使a∥b,则∠1与∠2应该满足什么关系式?请说明理由.

【答案】(1)a∥b(2)能(3)∠1+2∠2=180°
【解析】
(1)根据平行线的判定得出即可;
(2)求出∠1和∠4的度数,再根据平行线的判定推出即可;
(3)根据折叠得出∠3=∠4,根据平行线的性质得出∠1+∠3+∠4=180°,∠2=∠4,即可得出答案.
(1)a∥b,
理由是:∵∠1=∠2,
∴a∥b(内错角相等,两直线平行);
(2)能,
理由是:∵∠1=∠2,∠3=∠4,∠1+∠2=180°,∠3+∠4=180°,
∴∠1=∠2=90°,∠3=∠4=90°,
∴∠1=∠4,
∴a∥b;
(3)∠1+2∠2=180°,
理由是:根据折叠得:∠3=∠4,
∵a∥b,
∴∠1+∠3+∠4=180°,∠2=∠4,
∴∠1+2∠2=180°.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(﹣3,2).
(1)直接写出点E的坐标 ;
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t= 秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);
③当点P运动到CD上时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z之间的数量关系能否确定?若能,请用含x,y的式子表示z,写出过程;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).
(1)直接写出点A1,B1,C1的坐标.
(2)在图中画出△A1B1C1.
(3)连接AA1,求△AOA1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣4x+3.
(1)求函数图象的对称轴、顶点坐标、与坐标轴交点的坐标,并画出函数的大致图象;
(2)根据图象直接写出函数值y为负数时,自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的盒子里装有30个除颜色外其它均相同的球,其中红球有m个,白球有3m个,其它均为黄球.现小李从盒子里随机摸出一个球,若是红球,则小李获胜;小李把摸出的球放回盒子里摇匀,由小马随机摸出一个球,若为黄球,则小马获胜.
(1)当m=4时,求小李摸到红球的概率是多少?
(2)当m为何值时,游戏对双方是公平的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象经过坐标原点,与
的图象经过坐标原点,与![]() 轴的另一个交点为A(-2,0).
轴的另一个交点为A(-2,0).

(1)求二次函数的解析式
(2)在抛物线上是否存在一点P,使△AOP的面积为3,若存在请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李大爷以每千克2.1元的价格批发了一批南瓜到镇上出售,为了方便,他带了一些零钱备用,他先按市场价售出一些后,由于滞销,然后他每千克降低1.6元将剩余部分全部售出.他手中持有的钱数y元(含备用零钱)与售出南瓜千克数x的关系如图所示,下列说法中正确的有( )
①李大爷自带的零钱是50元
②降价前他每千克南瓜出售的价格是4.1元
③这批南瓜一共有160千克
④李大爷销售这批南瓜一共赚了194元

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
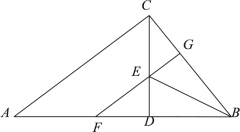
【题目】如图,在![]() 中,
中,![]() ,CD是高,BE平分∠ABC交CD于点E,EF∥AC交AB于点F,交BC于点G.在结论:(1)
,CD是高,BE平分∠ABC交CD于点E,EF∥AC交AB于点F,交BC于点G.在结论:(1) ![]()
![]() ;(2)
;(2) ![]() ;(3)
;(3)![]() ;(4)
;(4) ![]() 中,一定成立的有( )
中,一定成立的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com