
【题目】已知二次函数![]() .
.
(1)甲说:该二次函数的图象必定经过点![]() .乙说:若图象的顶点在x轴上,则
.乙说:若图象的顶点在x轴上,则![]() ,你觉得他们的结论对吗?请说明理由;
,你觉得他们的结论对吗?请说明理由;
(2)若抛物线经过![]() ,
,![]() ,求证
,求证![]() ;
;
(3)甲问乙:“我取的k是一个整数,画出它的图象后发现抛物线与x轴的一个交点在y轴右侧,一个交点在原点和![]() 之间,你知道k等于几吗?并求出k的值.
之间,你知道k等于几吗?并求出k的值.
【答案】(1)甲,乙的结论都错误,理由见解析;(2)证明见解析;(3)k=1
【解析】
(1)把函数表达式![]() 变形为y+3x2=k(x2-2x+6),求出当x=-2,y=-12时,
变形为y+3x2=k(x2-2x+6),求出当x=-2,y=-12时,![]() ,
,![]() ,可得结论;根据抛物线的顶点在x轴上得顶点的纵坐标为0从而可得k的值;
,可得结论;根据抛物线的顶点在x轴上得顶点的纵坐标为0从而可得k的值;
(2)将点P,Q的坐标分别代入二次函数解析式,得到含k的表达式,进行乘积运算,最后进行配方即可得到结论;
(3)分![]() 和
和 ![]() 两种情况分类讨论:当
两种情况分类讨论:当![]() 时,
时,![]() ,求得
,求得![]() ,此时无整数k;当
,此时无整数k;当![]() 时,根据
时,根据![]() 以及抛物线与x轴的一个交点在原点和
以及抛物线与x轴的一个交点在原点和![]() 之间可求得
之间可求得![]() ,从而求得整数k的值.
,从而求得整数k的值.
(1)∵![]()
∴![]()
当x=-2,y=-12时,![]() ,
,![]() ,
,
故该二次函数的图象不是必经过点![]() ,
,
因此,甲的结论不正确;
对于函数![]() 的顶点坐标为:(
的顶点坐标为:(![]() ,
, ![]() ),
),
∵图象的顶点在x轴上,
∴![]()
解得,![]() ,
,![]() ,
,
因此,图象的顶点在x轴上,则k=0或![]() ;
;
故乙的结论错误;
(2)把![]() ,
,![]() 分别代入
分别代入![]() 得,
得,
![]() ,
,![]() ,
,
∴![]() ,
,
∵![]()
∴![]() ;
;
(3)分两种情况:
(i)当![]() 时,即
时,即![]() ,由抛物线与x轴有两个交点得,
,由抛物线与x轴有两个交点得,
![]()
解得,![]() ,
,
∴![]() ,
,
∴不存在整数k;
(ii)当![]() 时,即
时,即![]() ,此时,
,此时, ![]() ,
,
∴![]() ,
,
∵抛物线与x轴的一个交点在原点和![]() 之间,
之间,
∴当x=-3时,y=![]() ,
,
解得,![]() ,
,
∴![]() ,
,
∴整数k=1.


科目:初中数学 来源: 题型:
【题目】已知抛物线Cn:yn=![]() x2+(n-1)x+2n (其中n为正整数)与x轴交于An,Bn.两点(点An在Bn的左边)与y轴交于点Dn.
x2+(n-1)x+2n (其中n为正整数)与x轴交于An,Bn.两点(点An在Bn的左边)与y轴交于点Dn.
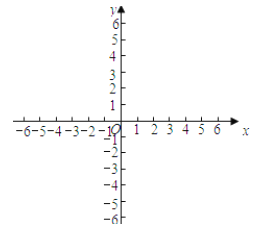
(1)填空:①当n=1时,点A1的坐标为______,点B1的坐标为______;
②当n=2时,点A2的坐标为______,点B2的坐标为______;
(2)猜想抛物线Cn是否经过某一个定点,若经过请写出该定点坐标并给予证明:若不经过,请说明理由;
(3)猜想![]() 的大小,并给予证明.
的大小,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
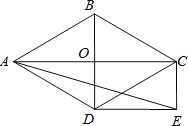
【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C. D作CE∥BD,DE∥AC,CE和DE交于点E.
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2![]() 时,求EA的长。
时,求EA的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
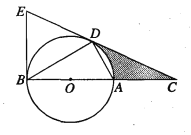
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为1,∠CBD=30°,则图中阴影部分的面积;
(3)过点B作⊙O的切线交CD的延长线于点E若BC=12,tan∠CDA=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=50°,圆O是△ABC的外接圆,AE为圆O的直径,AE与BC相交于点D,若AB=AD.则∠EAC=_______.
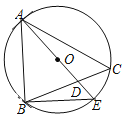
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:
(1)当轿车刚到乙地时,此时货车距离乙地 千米;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2020年初新冠肺炎疫情爆发以来,国内经济--度被按下暂停键,如今随着国内疫情防控形势持续向好,各地开始进人积极复工复产的新模式.某商家为降低疫情带来的影响,刺激消费,吸引顾客,特此设计了一个游戏,其规则是:分别转动如图所示的两个可以自由转动的转盘各一次,每次指针落在每一字母区域的机会均等(若指针恰好落在分界线上则重转),当两个转盘的指针所指字母相同时,消费者就可以获得一次八折优惠价购买商品的机会.
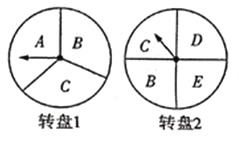
(1)用树状图或列表的方法表示出游戏可能出现的所有结果;
(2)若小亮参加一次游戏,则他能获得八折优惠价购买商品的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有3个分别写有数字﹣2,0,1的小球,它们除了数字不同以外其余完全相同,先从盒子里随机抽取1个小球,再从剩下的小球中抽取1个,将这两个小球上的数字依次记为a,b,则满足关于x的方程x2+ax+b=0有实数根的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰△ABC,∠ACB=120°,P是线段CB上一动点(与点C,B不重合),连接AP,延长BC至点Q,使得∠PAC=∠QAC,过点Q作射线QH交线段AP于H,交AB于点M,使得∠AHQ=60°.
(1)若∠PAC=α,求∠AMQ的大小(用含α的式子表示);
(2)用等式表示线段QC和BM之间的数量关系,并证明.
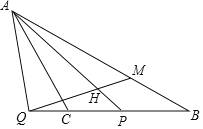
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com