
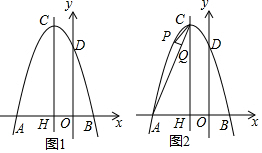
分析 (1)将点A(-3,0)、B(1,0)代入抛物线的解析式得到关于a、b的方程组即可;
(2)先求得C(-1,4).将D点向下平移1个单位,得到点M,连结AM交对称轴于F,作DE∥FM交对称轴于E点,则四边形BDEF周长的最小值=BD+EF+AM,然后求得直线AM的解析式,从而可求得点F的坐标,最后依据EF=1可得到点E的坐标;
(3)当△PCQ∽△ACH时,∠PCQ=∠ACH.过点A作CA的垂线交PC与点F,作FN⊥x轴与点N.则AF∥PQ,先证明△CPQ∽△CFA、△FNA∽△AHC,依据相似三角形的性质可求得AN=2,FN=1,则F(-5,1),然后再求得直线CF的解析式,将CF的解析式与抛物线的解析式联立组成方程组可求得点P的坐标.
解答 解:(1)∵抛物线y=ax2+bx+3过点A(-3,0),B(1,0),
∴$\left\{\begin{array}{l}{9a-3b+3=0}\\{a+b+3=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=-2}\end{array}\right.$,
∴抛物线的解析式为y=-x2-2x+3;
(2)∵y=-x2-2x+3=-(x+1)2+4,
∴顶点C(-1,4).
将D点向下平移1个单位,得到点M,连结AM交对称轴于F,作DE∥FM交对称轴于E点,如图1所示.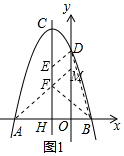
∵EF∥DM,DE∥FM,
∴四边形EFMD是平行四边形,
∴DE=FM,EF=DM=1,
DE+FB=FM+FA=AM.
由勾股定理,得AM=$\sqrt{O{A}^{2}+O{M}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,BD=$\sqrt{O{D}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
四边形BDEF周长的最小值=BD+DE+EF+FB=BD+EF+(DE+FB)=BD+EF+AM=$\sqrt{10}$+1+$\sqrt{13}$;
设AM的解析式为y=mx+n,将A(-3,0),M(0,2)代入,解得m=$\frac{2}{3}$,n=2,则AM的解析式为y=$\frac{2}{3}$x+2,
当x=-1时,y=$\frac{4}{3}$,即F(-1,$\frac{4}{3}$),
由EF=1,得E(-1,$\frac{7}{3}$).
故四边形BDEF的周长最小时,点E的坐标为(-1,$\frac{7}{3}$),点F坐标为(-1,$\frac{4}{3}$),四边形BDEF周长的最小值是$\sqrt{10}$+1+$\sqrt{13}$;
(3)点P在对称轴左侧,当△PCQ∽△ACH时,∠PCQ=∠ACH.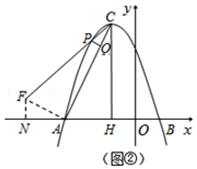
过点A作CA的垂线交PC与点F,作FN⊥x轴与点N.则AF∥PQ,
∴△CPQ∽△CFA,
∴$\frac{AC}{AF}$=$\frac{CH}{AH}$=2.
∵∠CAF=90°,
∴∠NAF+∠CAH=90°,∠NFA+∠NAF=90°,
∴∠BFA=∠CAH.
又∵∠FNA=∠AHC=90°,
∴△FNA∽△AHC,
∴$\frac{FN}{AH}$=$\frac{AN}{HC}$=$\frac{AF}{CA}$=$\frac{1}{2}$,即$\frac{AN}{4}$=$\frac{FN}{2}$=$\frac{1}{2}$.
∴AN=2,FN=1.
∴F(-5,1).
设直线CF的解析式为y=kx+b,将点C和点F的坐标代入得:$\left\{\begin{array}{l}{-k+b=4}\\{-5k+b=1}\end{array}\right.$,解得:k=$\frac{3}{4}$,b=$\frac{19}{4}$.
∴直线CF的解析式为y=$\frac{3}{4}$x+$\frac{19}{4}$.
将y=$\frac{3}{4}$x+$\frac{19}{4}$与y=-x2-2x+3联立得:$\left\{\begin{array}{l}{y=\frac{3}{4}x+\frac{19}{4}}\\{y=-{x}^{2}-2x+3}\end{array}\right.$解得:$\left\{\begin{array}{l}{x=-\frac{7}{4}}\\{y=\frac{55}{16}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$(舍去).
∴P(-$\frac{7}{4}$,$\frac{55}{16}$).
∴满足条件的点P的坐标为(-$\frac{7}{4}$,$\frac{55}{16}$).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式、相似三角形的性质和判定、轴对称的性质,找出四边形BDEF周长取得最小值的条件是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 了解全市高三年级学生的睡眠质量 | |
| B. | 了解我校同学对国家设立雄安新区的看法 | |
| C. | 对端午出游旅客上飞机前的安全检查 | |
| D. | 对电影“摔跤吧,爸爸”收视率的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
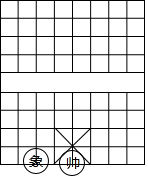 如图,中国象棋中对“象”的走法有一定的限制,只能走“田”字.若此时“象”的坐标为(-2,-4)“帅”的坐标为(0,-4),试写出此“象”下一步可能走到的各位置的坐标.
如图,中国象棋中对“象”的走法有一定的限制,只能走“田”字.若此时“象”的坐标为(-2,-4)“帅”的坐标为(0,-4),试写出此“象”下一步可能走到的各位置的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
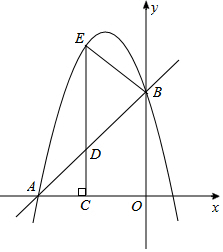 如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,抛物线y=-x2+bx+c过A、B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.
如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,抛物线y=-x2+bx+c过A、B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com