
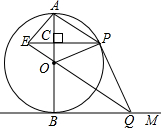
 如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP.
如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP.分析 (1)根据切线的性质得∠OBQ=90°,再根据平行线的性质得∠APO=∠POQ,∠OAP=∠BOQ,加上∠OPA=∠OAP,则∠POQ=∠BOQ,于是根据“SAS”可判断△BOQ≌△POQ;
(2)①利用△BOQ≌△POQ得到∠OPQ=∠OBQ=90°,由于OB=OP,所以当∠BOP=90°,四边形OPQB为正方形,此时点C、点E与点O重合,于是PE=PO=6;②根据菱形的判定,当OC=AC,PC=EC,四边形AEOP为菱形,则OC=$\frac{1}{2}$OA=3,然后利用勾股定理计算出PC,从而得到PE的长.
解答 (1)证明:∵BM切⊙O于点B,
∴OB⊥BQ,
∴∠OBQ=90°,
∵PA∥OQ,
∴∠APO=∠POQ,∠OAP=∠BOQ,
而OA=OP,
∴∠OPA=∠OAP,
∴∠POQ=∠BOQ,
在△BOQ和△POQ中
$\left\{\begin{array}{l}{OB=OP}\\{∠BOQ=∠POQ}\\{OQ=OQ}\end{array}\right.$,
∴△BOQ≌△POQ;
(2)解:①∵△BOQ≌△POQ,
∴∠OPQ=∠OBQ=90°,
当∠BOP=90°,四边形OPQB为矩形,
而OB=OP,则四边形OPQB为正方形,此时点C、点E与点O重合,PE=PO=$\frac{1}{2}$AB=6;
②∵PE⊥AB,
∴当OC=AC,PC=EC,四边形AEOP为菱形,
∵OC=$\frac{1}{2}$OA=3,
∴PC=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∴PE=2PC=6$\sqrt{3}$.
故答案为6,6$\sqrt{3}$.
点评 本题考查了圆的综合题:熟练掌握切线的性质、全等三角形的判定与性质和菱形、正方形的判定方法;会利用勾股定理计算线段的长.


科目:初中数学 来源: 题型:解答题
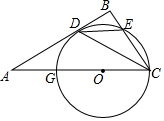 如图,点O为Rt△ABC斜边AC上一点,以点O为圆心,OC长为半径的⊙O与AB相切于点D,分别交AC,BC于点G,E.
如图,点O为Rt△ABC斜边AC上一点,以点O为圆心,OC长为半径的⊙O与AB相切于点D,分别交AC,BC于点G,E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,动点D从点A出发,沿线段AC以每秒1个单位的速度向终点C运动,动点E同时从点B出发,以每秒2个单位的速度沿射线BC方向运动,当点D停止时,点E也随之停止,连结DE,当C、D、E三点不在同一直线上时,以ED、EC我邻边作?ECFD,设点D运动的时间为t(秒).
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,动点D从点A出发,沿线段AC以每秒1个单位的速度向终点C运动,动点E同时从点B出发,以每秒2个单位的速度沿射线BC方向运动,当点D停止时,点E也随之停止,连结DE,当C、D、E三点不在同一直线上时,以ED、EC我邻边作?ECFD,设点D运动的时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,第一象限内的点A、B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且tan∠ACB=$\frac{2}{3}$
如图,第一象限内的点A、B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且tan∠ACB=$\frac{2}{3}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
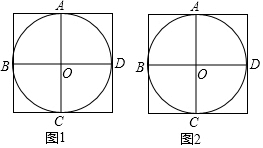 在图1、图2中,⊙O经过了正方形网格中的格点A、B、C、D,现请你仅用无刻度的直尺分别在图1、图2中画出一个满足下列条件的∠P.
在图1、图2中,⊙O经过了正方形网格中的格点A、B、C、D,现请你仅用无刻度的直尺分别在图1、图2中画出一个满足下列条件的∠P.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
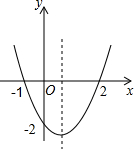 二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为($\frac{1}{2}$,-2);⑤当x<$\frac{1}{2}$时,y随x的增大而减小;⑥a+b+c>0正确的有( )
二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为($\frac{1}{2}$,-2);⑤当x<$\frac{1}{2}$时,y随x的增大而减小;⑥a+b+c>0正确的有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com