
分析 (1)由m=24,摸到黑球的概率不少于$\frac{1}{2}$,根据题意可得$\frac{21-3x}{24}$≥$\frac{1}{2}$,继而求得答案;
(2)由若m=$\frac{50}{7-x}$,摸到白种球概率的最大,可得$\frac{x+3}{\frac{50}{7-x}}$=$\frac{(x+3)(7-x)}{50}$=$\frac{-(x-2)^{2}+25}{50}$,则可求得x的值,继而求得答案.
解答 解:(1)∵口袋中有三个颜色的球共m个,其中白球x+3个,红球2x个,m=24,
∴黑球有:24-(x+3)-2x=21-3x,
∵摸到黑球的概率不少于$\frac{1}{2}$,
∴$\frac{21-3x}{24}$≥$\frac{1}{2}$,
解得:x≤3,
∴口袋中的红球的个数最多6个;
(2)∵m=$\frac{50}{7-x}$,白球x+3,
∴摸到白种球概率为:$\frac{x+3}{\frac{50}{7-x}}$=$\frac{(x+3)(7-x)}{50}$=$\frac{-(x-2)^{2}+25}{50}$,
∴当x=2时,摸到白种球概率的最大,
∴m=10,白球5个,红球4个,
∴袋中黑球有:10-5-4=1(个);
∴若m=$\frac{50}{7-x}$,当摸到白种球概率的最大时,袋中黑球有1个.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{4}$=±2 | B. | $\sqrt{{3^2}+{4^2}}$=7 | C. | $\sqrt{(-\frac{1}{2}}{)^2}=-\frac{1}{2}$ | D. | $\sqrt{2\frac{1}{4}}=1\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
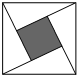 “赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.学习《探索勾股定理》后,几位同学在上课用的道具上玩掷骰子的游戏,看谁能把骰子投到中间的小正方形中.若设直角三角形的两条直角边的长分别是1和2.你能算出骰子投在在中间小正方形区域(含边线)的概率吗?是$\frac{1}{5}$.
“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.学习《探索勾股定理》后,几位同学在上课用的道具上玩掷骰子的游戏,看谁能把骰子投到中间的小正方形中.若设直角三角形的两条直角边的长分别是1和2.你能算出骰子投在在中间小正方形区域(含边线)的概率吗?是$\frac{1}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com