
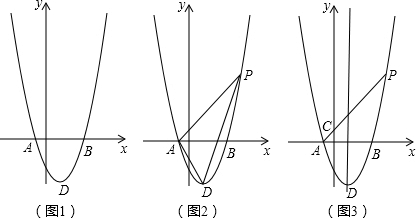
���� ��1���������A��B�������꣬�Ƴ���������D��1��-4�����������ߵĽ���ʽ���a���ɣ�
��2������A��-1��0����C��0��t�������������ֱ��AP�Ľ���ʽ�����÷����������P���꣬�ٸ���S=S��AKD+S��PKD���㼴�ɣ�
��3������ֱ��PG�Ľ���ʽΪy=-tx+b�䣬��P��t+3��t2+4t��������õ�b��=2t2+7t���Ƴ�ֱ��PG�Ľ���ʽΪy=-tx+2t2+7t����$\left\{\begin{array}{l}{y={x}^{2}-2x-3}\\{y=-tx+2{t}^{2}+7t}\end{array}\right.$�����$\left\{\begin{array}{l}{x=t+3}\\{y={t}^{2}+4t}\end{array}\right.$��$\left\{\begin{array}{l}{x=-2t-1}\\{y=4{t}^{2}+8t}\end{array}\right.$���Ƴ���G���꣨-2t-1��4t2+8t�����Ƴ�PE=t+2��GH=2t+2����PE•GH=12���õ���t+2����2t+2��=12���Ƴ�P��4��5����ֱ��AP�Ľ���ʽΪy=x+1����M��m��m2-2m-3������N��m��m+1��������AN=MN�г����̼��ɽ�����⣮
��� �⣺��1������������y=ax2-2ax-3a����y=0���õ�ax2-2ax-3a=0�����x=-1��3��
��A��-1��0����B��3��0����
�������ߵĶԳ���x=1������D����Ϊ��1��-4����
��D��1��-4������y=ax2-2ax-3a���õ�a=1��
�������ߵĽ���ʽΪy=x2-2x-3��
��2����ͼ2�У���PA�������ߵĶԳ��ύ�ڵ�K��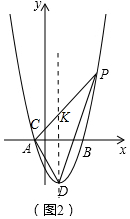
��ֱ��AP�Ľ���ʽΪy=kx+b����A��-1��0����C��0��t������õ�$\left\{\begin{array}{l}{b=t}\\{-k+b=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=t}\\{b=t}\end{array}\right.$��
��ֱ��AP�Ľ���ʽΪy=tx+t��
��$\left\{\begin{array}{l}{y=tx+t}\\{y={x}^{2}-2x-3}\end{array}\right.$���$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$��$\left\{\begin{array}{l}{x=t+3}\\{y={t}^{2}+4t}\end{array}\right.$��
���P���꣨t+3��t2+4t����K��1��2t����
��S=S��AKD+S��PKD=$\frac{1}{2}$•��2t+4��•��t+3+1��=t2+6t+8��t��0����
��3����ͼ3�У�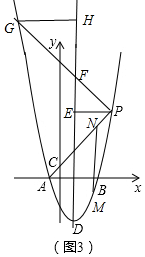
��PE�������ߵĶԳ��ᣬPG��PA����PE�Գƣ�
����Լ���ֱ��PG�Ľ���ʽΪy=-tx+b�䣬��P��t+3��t2+4t��������õ�b��=2t2+7t��
��ֱ��PG�Ľ���ʽΪy=-tx+2t2+7t��
��$\left\{\begin{array}{l}{y={x}^{2}-2x-3}\\{y=-tx+2{t}^{2}+7t}\end{array}\right.$�����$\left\{\begin{array}{l}{x=t+3}\\{y={t}^{2}+4t}\end{array}\right.$��$\left\{\begin{array}{l}{x=-2t-1}\\{y=4{t}^{2}+8t}\end{array}\right.$��
���G���꣨-2t-1��4t2+8t����
��PE=t+2��GH=2t+2��
��PE•GH=12��
�ࣨt+2����2t+2��=12��
��t=1��-4����������
��P��4��5����ֱ��AP�Ľ���ʽΪy=x+1����M��m��m2-2m-3������N��m��m+1��
��AN=NM��
��$\sqrt{2}$��m+1��=m+1-��m2-2m+3����
��m2+��$\sqrt{2}$-3��m+$\sqrt{2}$-4=0��
�ࣨm+1����m+$\sqrt{2}$-4��=0��
��m=4-$\sqrt{2}$��-1����������
���M�ĺ�����Ϊ4-$\sqrt{2}$��
���� ���⿼����κ����ۺ��⡢һ�κ�����������������������֪ʶ������Ĺؼ���ѧ�����ò�����ѧ���÷���������������ͼ��Ľ������꣬ѧ�������ת��Ϊ���̽���������п�ѹ���⣮


 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
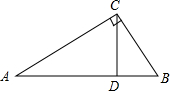 ��ͼ���ڡ�ABC�У���ACB=90�㣬��A=30�㣬CD��AB��AB=8����BC=4����BCD=30�㣬BD=2��
��ͼ���ڡ�ABC�У���ACB=90�㣬��A=30�㣬CD��AB��AB=8����BC=4����BCD=30�㣬BD=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
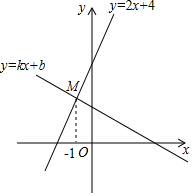 ��ͼ����ֱ֪��y=2x+4��ֱ��y=kx+b���ڵ�M��-1��a���������x��y�Ķ�Ԫһ�η�����$\left\{\begin{array}{l}{2x-y+4=0}\\{kx-y+b=0}\end{array}\right.$�Ľ�Ϊ$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$��
��ͼ����ֱ֪��y=2x+4��ֱ��y=kx+b���ڵ�M��-1��a���������x��y�Ķ�Ԫһ�η�����$\left\{\begin{array}{l}{2x-y+4=0}\\{kx-y+b=0}\end{array}\right.$�Ľ�Ϊ$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com