
【题目】如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1,以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,......,按此规律继续下去,则矩形AB2019C2019C2018的面积为_____.

【答案】![]()
【解析】
利用勾股定理可求得AC的长,根据面积比等于相似比的平方可得矩形AB1C1C的面积,同理可求出矩形AB2C2C1、AB3C3C2,……的面积,从而可发现规律,根据规律即可求得第2019个矩形的面积,即可得答案.
∵在矩形ABCD中,AD=2,CD=1,
∴AC=![]() =
=![]() ,
,
∵矩形ABCD与矩形AB1C1C相似,
∴矩形AB1C1C与矩形ABCD的相似比为![]() ,
,
∴矩形AB1C1C与矩形ABCD的面积比为![]() ,
,
∵矩形ABCD的面积为1×2=2,
∴矩形AB1C1C的面积为2×![]() =
=![]() ,
,
同理:矩形AB2C2C1的面积为![]() ×
×![]() =
=![]() =
=![]() ,
,
矩形AB3C3C2的面积为![]() ×
×![]() =
=![]() =
=![]() ,
,
……
∴矩形ABnCnCn-1面积为![]() ,
,
∴矩形AB2019C2019C2018的面积为![]() =
=![]() ,
,
故答案为:![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】2016年3月国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润W最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区平面图如图1所示,![]() 为边界上的点.已知边界
为边界上的点.已知边界![]() 是一段抛物线,其余边界均为线段,且
是一段抛物线,其余边界均为线段,且![]() ,抛物线顶点
,抛物线顶点![]() 到
到![]() 的距离
的距离![]() .以
.以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系.
轴,建立平面直角坐标系.
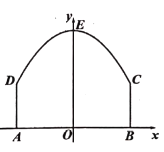
![]() 求边界
求边界![]() 所在抛物线的解析式;
所在抛物线的解析式;
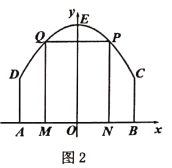
![]() 如图2,该景区管理处欲在区域
如图2,该景区管理处欲在区域![]() 内围成一个矩形
内围成一个矩形![]() 场地,使得点
场地,使得点![]() 在边界
在边界![]() 上,点
上,点![]() 在边界
在边界![]() 上,试确定点
上,试确定点![]() 的位置,使得矩形
的位置,使得矩形![]() 的周长最大,并求出最大周长.
的周长最大,并求出最大周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊至B′处,紧绷着的吊缆A′B′=AB.AB垂直地面O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA=![]() ,sinA′=
,sinA′=![]() .
.

(1)求此重物在水平方向移动的距离BC;
(2)求此重物在竖直方向移动的距离B′C.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
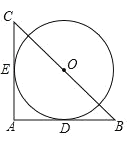
【题目】如图,在 Rt△ABC 中BC=2![]() ,以 BC 的中点 O 为圆心的⊙O 分别与 AB,AC 相切于 D,E 两点,
,以 BC 的中点 O 为圆心的⊙O 分别与 AB,AC 相切于 D,E 两点,![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.πD.2π
C.πD.2π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 是
是![]() 边上的一点,
边上的一点,![]() ,
,![]() ,将正方形边
,将正方形边![]() 沿
沿![]() 折叠到
折叠到![]() ,延长
,延长![]() 交
交![]() 于
于![]() .连接
.连接![]() ,现在有如下四个结论:①
,现在有如下四个结论:①![]() ;②
;②![]() ;③
;③![]() ∥
∥![]() ;④
;④![]() ; 其中结论正确的个数是( )
; 其中结论正确的个数是( )

A.1B.2
C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
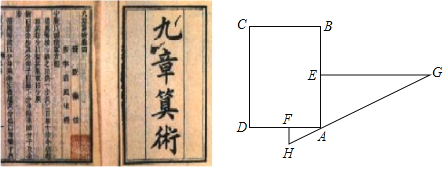
【题目】《九章算术》是中国古代第一部数学专著,是《算经十书》中最重要的一种,成于公元一世纪左右.在其“勾股”章中有这样一个问题:“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD.EG=15里,HG经过点A,则FH等于多少里?请你根据上述题意,求出FH的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y1=x+m的图象与反比例函数y2=![]() 的图象相交于A(﹣1,﹣3)和点B,且与x轴交于点C.
的图象相交于A(﹣1,﹣3)和点B,且与x轴交于点C.
(1)求m及k的值.
(2)求点B、C坐标,并结合图形直接写出不等式0<x+m<![]() 的解集.
的解集.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com