
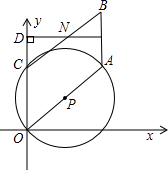 A、B两点不重合),点N是DM与BC的交点,设OD=t;
A、B两点不重合),点N是DM与BC的交点,设OD=t;| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| PE2+GE2 |
| t2-t+1 |
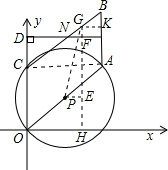 解:(1)连接AC.
解:(1)连接AC.| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| PE2+GE2 |
(
|
| t2-t+1 |
| t2-t+1 |
| 8 |
| 5 |
| 8 |
| 5 |
| 8 |
| 5 |
| 3 |
| 5 |
| 3 |
| OD+AM |
| 2 |
(
| ||||
| 2 |
| 3 |
| 11 |
| 10 |
| 3 |


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
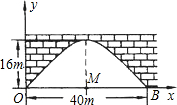 如图,有一个抛物线的拱形立交桥,这个桥拱的最大高度为16m,跨度为40m,现把它放在如图所示的直角坐标系里,若要在离跨度中心点M5m处垂直竖一根铁柱支撑这个拱顶,铁柱应取多长?
如图,有一个抛物线的拱形立交桥,这个桥拱的最大高度为16m,跨度为40m,现把它放在如图所示的直角坐标系里,若要在离跨度中心点M5m处垂直竖一根铁柱支撑这个拱顶,铁柱应取多长?查看答案和解析>>
科目:初中数学 来源:学习周报 数学 北师大八年级版 2009-2010学年 第19-26期 总第175-182期 北师大版 题型:044
在如图所示的直角坐标平面上,表示下列各点:
(4,4),(1,4),(3,2),(8,2),(10,4),(4,4),(4,8),(8,7),(8,5),(4,6).
(1)用线段依次按照上述顺序把各点连接起来形成一个图案,这个图案像什么?
(2)把这些点的横坐标都加5,纵坐标不变,想象由这些点顺次连接形成的图案与(1)中的图案有什么关系?
(3)把题目中各点的横坐标不变,纵坐标都乘以-1,重新在图中描点、连线,得到的图案与(1)中的图案有什么关系?
查看答案和解析>>
科目:初中数学 来源:《第2章 二次函数》2010年单元测试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省湖州市吴兴区九年级(上)第一次月考数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:《第2章 二次函数》2010年单元测试2(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com