
����Ŀ����ͼ�� �ı���OABCΪֱ�����Σ�A��4��0����B��3��4����C��0��4���� ��![]() ��
��![]() ������ÿ��2����λ���ȵ��ٶ���
������ÿ��2����λ���ȵ��ٶ���![]() �˶�����
�˶�����![]() ��
��![]() ͬʱ��������ÿ��1����λ���ȵ��ٶ���
ͬʱ��������ÿ��1����λ���ȵ��ٶ���![]() �˶�������һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ�˶�������
�˶�������һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ�˶�������![]() ��
��![]() ��ֱ
��ֱ![]() ���ڵ�
���ڵ�![]() ������AC��NP��Q������MQ��
������AC��NP��Q������MQ��

��1���� ����M��N���ܵ����յ㣻
��1�����AQM�����S���˶�ʱ��t�ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ����tΪ��ֵʱ��S��ֵ���
��1���Ƿ���ڵ�M��ʹ�á�AQMΪֱ�������Σ������ڣ������M�����꣬�������ڣ�
![]() ˵�����ɣ�
˵�����ɣ�
���𰸡�
��1����M
��1������t��ʱ��![]() ��
�� ![]() ����
����![]() ��
��![]()
��![]() =
=![]() =
=![]() ����
����![]() ��
��![]()
��![]()
![]()
�� ��
��![]() �൱
�൱![]() ʱ��S��ֵ���
ʱ��S��ֵ���
��1�����ڡ�
�辭��t��ʱ��NB=t��OM=2t ����![]() ��
��![]() ��
��![]() =
=![]() =
=![]()
����![]() ����
����![]() �ǵ���Rt��
�ǵ���Rt��![]() �ױ�
�ױ�![]() �ϵĸߣ�
�ϵĸߣ�
��![]() �ǵױ�
�ǵױ�![]() ������ ��
������ ��![]() ����
����![]() ����
����![]() �� ���
�� ���![]() ��������1��0��
��������1��0��
����![]() ����ʱ
����ʱ![]() ��
��![]() �غϣ���
�غϣ���![]() ����
����![]() ��
��
��![]() ���
���![]() ��������2��0��
��������2��0��
��������
��1�����ڵ�M�ȵ�N�ȳ������ҵ�M���ٶȱȵ�N��֪��M�ܵ����յ㣮
��1������t��ʱ�ɵ�NB=y��OM-2t��������BCA=��MAQ=45���Ƴ�QN=CN��PQ��ֵ�����S��t�ĺ�����ϵʽ�����t��ֵ���S�����ֵ��
��1�����������������ۣ�����AQM=90����PQ�ǵ���Rt��MQA�ױ�MA�ϵĸߣ�
����QMA=90����QM��QP�غϣ����tֵ��


 Сѧ���AB��ϵ�д�
Сѧ���AB��ϵ�д� ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=mx+n��m��0����ͼ���뷴��������y=![]() ��k��0����ͼ���ڵ�һ���������ڵ�A��B���㣬��y�ύ�ڵ�C������B��BM��x�ᣬ����ΪM��BM=OM��OB=2
��k��0����ͼ���ڵ�һ���������ڵ�A��B���㣬��y�ύ�ڵ�C������B��BM��x�ᣬ����ΪM��BM=OM��OB=2![]() ����A��������Ϊ4��
����A��������Ϊ4��
��1����÷�����������һ�κ����Ľ���ʽ��
��2������MC�����ı���MBOC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��֣������������ȥũó�г�����̯����֣���̵�Ҫ���õ��ӳӳ���5ǧ�˼�����֣���̻����������ԣ��Ѽ��������Դ�������Ϊ0.6ǧ�˵������У���������ȷ����Ҫ����ڵ��ӳ����ٳ�һ�飬�Ƶ�Ϊ5.75ǧ�ˣ��ϰ������˵������ȥ���Ӻ�Ϊ5.15ǧ�ˣ��Ϲ˿�������0.15ǧ�˾����ˡ���֣���̸��˵ظ���Ǯ������ػؼ��ˡ�����˵����ȷ���ǣ� ��

A.֣�����ˣ�������ʵ������Ϊ5.15ǧ��
B.֣���̿��ˣ�������ʵ������Ϊ4ǧ��
C.֣���̿��ˣ�������ʵ������Ϊ4.85ǧ��
D.֣���̲���Ҳ����������ʵ������Ϊ5ǧ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ���������λͬѧ����һ��ƹ���������Ҫ����ѡ����λͬѧ����һ��������
��1��������״ͼ�����б�������ǡ��ѡ�мס�����λͬѧ�ĸ��ʣ�
��2������ȷ���״��һ�����ٴ�������λͬѧ�����ѡȡһλ����ǡ��ѡ����ͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
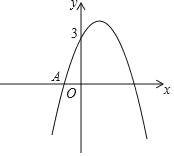
����Ŀ����ͼ����֪���κ���y=ax2+bx+3��ͼ�����A����1��0������������Ϊ��1��m����
��1����ö��κ����Ĺ�ϵʽ��mֵ��
��2�����ͼ����������⣺��ֱ��д���𰸣�
����xȡʲôֵʱ���ú�����ͼ����x���·���
������1��x��2ʱ��ֱ��д������y��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������棺��¿��װ30��,ÿ���ۼ�300Ԫ.��һ���Թ�����10��ʱ,�ۼ۲��䣻��һ���Թ���10��ʱ��ÿ����1���������ÿ����װ���ۼ۾�����3Ԫ����֪�÷�װ�ɱ���ÿ��200Ԫ����˿�һ���Թ����װx��ʱ����������л���yԪ��
��1����y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2���˿�һ���Թ�����ټ�ʱ����������л�����ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
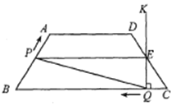
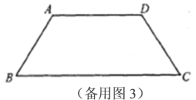
����Ŀ����ͼ���ڵ�������ABCD�У�![]() ��
��![]() ��
��![]() ��
��![]() .�����ӵ�B���������߶�
.�����ӵ�B���������߶�![]() ��ÿ��5����λ�����ٶ����C�����˶�����Q�ӵ�C�������߶�CB������ÿ��3����λ�����ٶ������˶�������O����������OKIBC�������߶�
��ÿ��5����λ�����ٶ����C�����˶�����Q�ӵ�C�������߶�CB������ÿ��3����λ�����ٶ������˶�������O����������OKIBC�������߶�![]()
![]() �ڵ�E����P��Oͬʱ��ʼ�˶���Ϊ�������C�غ�ʱֹͣ�˶�����QҲ��ֹ֮ͣ.���P��Q�˶���ʱ����t��
�ڵ�E����P��Oͬʱ��ʼ�˶���Ϊ�������C�غ�ʱֹͣ�˶�����QҲ��ֹ֮ͣ.���P��Q�˶���ʱ����t��![]() .
.
��1����P�����յ�Cʱ����t��ֵ����ָ����ʱBQ�ij���
��2���������˶���AD��ʱ��tΪ��ֵ��ʹ![]() ��
��
��3��tΪ��ֵʱ���ĵ�P��Q��C��E��Ϊһ��ƽ���ı��εĶ��㣿
��4��![]() ��Ϊֱ��������ʱt��ȡֵ��Χ________.��ֱ��д�������
��Ϊֱ��������ʱt��ȡֵ��Χ________.��ֱ��д�������
��ע������ͼ�����ÿ������⻭��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���İְ���һ�����˾����һ������С���İְ���ij����Ϊ�����㣬�ڶ�������Ĺ�·����Ӫ������Ϊ��������Ϊ�������Ⱥ�����¼���£�����λkm��
+5����3����5��+4����8��+6����4
��1�������һ���˿��͵�Ŀ�ĵ�ʱ�������������ж�Զ��������ʲô����
��2����ÿǧ���շ�Ϊ2Ԫ��С���ְ���������Ӫҵ���Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��y�Ķ�Ԫһ�η���ax+b��y��a��bΪ������a��0��
��1���÷��̵Ľ����� ���飻��a����2��b��6����x��yΪ�Ǹ���������ֱ��д���÷��̵Ľ⣻
��2����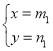 ��
��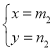 �Ǹ÷��̵�����⣬��m1��m2
�Ǹ÷��̵�����⣬��m1��m2
����n1��n2��2��m2��m1������a��ֵ��
����m1+m2��3b��n1+n2��ab+4����b��2����Ƚ�n1��n2��С����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com