
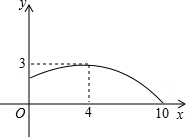
 如图,一学生推铅球时,铅球行进高度y(m)与水平距离x(m)的函数图象为抛物线.
如图,一学生推铅球时,铅球行进高度y(m)与水平距离x(m)的函数图象为抛物线.分析 (1)铅球推出的距离是抛物线与x轴交点的横坐标,由图直接获得答案即可.
(2)已知抛物线的顶点坐标,可设其解析式为顶点式,有因为点(10,0)在该抛物线的图象上,可将该点的坐标代入求得抛物线的解析式.
(3)利用(2)求得的抛物线的解析式,令x=0,求出对应的y的值即就是铅球推出的距离是.
解答 解:(1)∵抛物线与x轴的交点的横坐标为10,
即当铅球行进的高度为0米是,其水平距离为10米
∴铅球推出的距离是10米
(2)∵抛物线的顶点坐标为(4,3)
∴可设抛物线的解析式为:y=a(x-4)2+3
∵点(10,0)在该抛物线上,
∴0=a(10-4)2+3
解之得:a=-$\frac{1}{12}$
∴所求抛物线的解析式为:y=-$\frac{1}{12}$(x-4)2+3
(3)令x=0,则由抛物线的解析式得:y=-$\frac{1}{12}$×16+3=$\frac{5}{3}$
即该同学铅球出手处的坐标为(0,$\frac{5}{3}$)
点评 本题考查了二次函数的应用,解题的关键是理解抛物线上特殊的点与实际问题的关系.


科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合),BE的垂直平分线交AB于M,交DC于N,设AE=x.
如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合),BE的垂直平分线交AB于M,交DC于N,设AE=x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
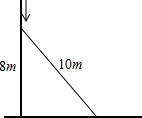 一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.
一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(+2.7)=-2.7 | B. | +(-8)=-8 | C. | -(-$\frac{1}{2}$)=-$\frac{1}{2}$ | D. | +(+4)=+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
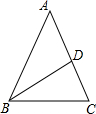 如图,△ABC中,∠A=46°,∠C=74°,BD平分∠ABC,交AC于点D,那么∠BDC的度数是( )
如图,△ABC中,∠A=46°,∠C=74°,BD平分∠ABC,交AC于点D,那么∠BDC的度数是( )| A. | 76° | B. | 81° | C. | 92° | D. | 104° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com