

分析 (1)根据已知条件及互余关系,可证△CAD≌△BCE,得出CD=BE,CE=AD,由DE=CD+CE,得出线段DE=BE+AD.
(2)过点C作直线l,在直线l上取点D和点E,使得∠ADC=∠BEC=∠ACB=α,先证△CAD≌△BCE,得出CD=BE,CE=AD,由DE=CD+CE,得出线段DE=BE+AD.
解答 解:(1)如图1,∵AD⊥l,BE⊥l,
∴∠CDA=∠BEC=90°,∠ACD+∠CAD=90°,
∵∠C=90°,
∴∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△CAD和△BCE中,
$\left\{\begin{array}{l}{∠CAD=∠BCE}\\{∠CDA=∠BEC}\\{AC=CB}\end{array}\right.$,
∴△CAD≌△BCE(AAS),
∴CD=BE,CE=AD,
又∵DE=CD+CE,
∴DE=BE+AD.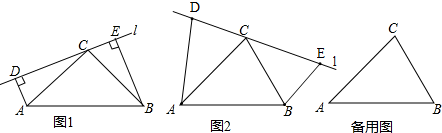
(2)如图2,过点C作直线l,在直线l上取点D和点E,使得∠ADC=∠BEC=∠ACB=α,则
∠ACD+∠BCE=180°-α,∠ACD+∠CAD=180°-α,
∴∠BCE=∠CAD,
在△CAD和△BCE中,
$\left\{\begin{array}{l}{∠CAD=∠BCE}\\{∠CDA=∠BEC}\\{AC=CB}\end{array}\right.$,
∴△CAD≌△BCE(AAS),
∴CD=BE,CE=AD,
又∵DE=CD+CE,
∴DE=BE+AD.
点评 本题主要考查了全等三角形的判定与性质,解决问题的关键是掌握:两角及其中一个角的对边对应相等的两个三角形全等.全等三角形的判定与全等三角形的性质是证明线段相等或角相等的重要工具.


科目:初中数学 来源: 题型:解答题
 甲、乙两个物流公司分别在A、B两地之间进行货物交换,C地为两车的货物中转站,假设A、B、C三地在同一条直线上,甲车以120km/h的速度从A地出发赶往C地,乙车从B地出发也赶往C地,两车同时出发,在C地利用一段时间交换货物,然后各自按原速返回自己的出发地,假设两车在行驶过程中各自速度保持不变,设两车行驶的时间为x(h),两车的距离为y(km),图中的折线表示y与x之间的函数关系.
甲、乙两个物流公司分别在A、B两地之间进行货物交换,C地为两车的货物中转站,假设A、B、C三地在同一条直线上,甲车以120km/h的速度从A地出发赶往C地,乙车从B地出发也赶往C地,两车同时出发,在C地利用一段时间交换货物,然后各自按原速返回自己的出发地,假设两车在行驶过程中各自速度保持不变,设两车行驶的时间为x(h),两车的距离为y(km),图中的折线表示y与x之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等边三角形ABC中,E、D分别在AB、AC上,若AD=BE,且CE、BD交于点O,CF⊥BD于F.
如图,等边三角形ABC中,E、D分别在AB、AC上,若AD=BE,且CE、BD交于点O,CF⊥BD于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用圆规、直尺作图,不写作法.但要保留作图痕迹.
用圆规、直尺作图,不写作法.但要保留作图痕迹.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com