
【题目】如图,矩形ABCD中,点E为BC上一点,F为DE的中点,且∠BFC=90°.
(1)当E为BC中点时,求证:△BCF≌△DEC;
(2)当BE=2EC时,求 ![]() 的值;
的值;
(3)设CE=1,BE=n,作点C关于DE的对称点C′,连结FC′,AF,若点C′到AF的距离是 ![]() ,求n的值.
,求n的值.
【答案】
(1)
证明;∵在矩形ABCD中,∠DCE=90°,F是斜边DE的中点,
∴CF= ![]() DE=EF,
DE=EF,
∴∠FEC=∠FCE,
∵∠BFC=90°,E为BC中点,
∴EF=EC,
∴CF=CE,
在△BCF和△DEC中, 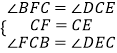 ,
,
∴△BCF≌△DEC(ASA)
(2)
解:设CE=a,由BE=2CE,得:BE=2a,BC=3a,
∵CF是Rt△DCE斜边上的中线,
∴CF= ![]() DE,
DE,
∵∠FEC=∠FCE,∠BFC=∠DCE=90°,
∴△BCF∽△DEC,
∴ ![]() ,
,
即: ![]() =
= ![]() ,
,
解得:ED2=6a2,
由勾股定理得:DC= ![]() =
= ![]() =
= ![]() a,
a,
∴ ![]() =
= ![]() =
= ![]()
(3)
解:过C′作C′H⊥AF于点H,连接CC′交EF于M,如图所示:

∵CF是Rt△DCE斜边上的中线,
∴FC=FE=FD,
∴∠FEC=∠FCE,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∴∠ADF=∠CEF,
∴∠ADF=∠BCF,
在△ADF和△BCF中,  ,
,
∴△ADF≌△BCF(SAS),
∴∠AFD=∠BFC=90°,
∵CH⊥AF,C′C⊥EF,∠HFE=∠C′HF=∠C′MF=90°,
∴四边形C′MFH是矩形,
∴FM=C′H= ![]() ,
,
设EM=x,则FC=FE=x+ ![]() ,
,
在Rt△EMC和Rt△FMC中,
由勾股定理得:CE2﹣EM2=CF2﹣FM2,
∴12﹣x2=(x+ ![]() )2﹣(
)2﹣( ![]() )2,
)2,
解得:x= ![]() ,或x=﹣
,或x=﹣ ![]() (舍去),
(舍去),
∴EM= ![]() ,FC=FE=
,FC=FE= ![]() +
+ ![]() ;
;
由(2)得: ![]() ,
,
把CE=1,BE=n代入计算得:CF= ![]() ,
,
∴ ![]() =
= ![]() +
+ ![]()
解得:n=4
【解析】本题是四边形综合题目,考查了矩形的性质与判定、全等三角形的判定与性质、直角三角形斜边上的中线性质、勾股定理、相似三角形的判定与性质、等腰三角形的判定与性质等知识;本题综合性强,难度较大,证明三角形全等和三角形相似是解决问题的关键.
【考点精析】利用直角三角形斜边上的中线和平行四边形的判定与性质对题目进行判断即可得到答案,需要熟知直角三角形斜边上的中线等于斜边的一半;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是cm.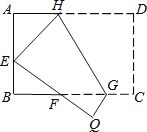
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=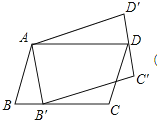
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=1,AD=![]() ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )
,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )
A.②③
B.③④
C.①②④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,使点C落在点C的位置,则图中的一个等腰直角三角形是( )
A.△ADC′
B.△BDC′
C.△ADC
D.不存在
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论正确的是( )
A.x2﹣2是二次二项式
B.单项式﹣x2的系数是1
C.使式子 ![]() 有意义的x的取值范围是x>﹣2
有意义的x的取值范围是x>﹣2
D.若分式 ![]() 的值等于0,则a=±1
的值等于0,则a=±1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com