
| 分 组(m) | 频数(名) | 频率 |
| 1.565~1.595 | 2 | 0.04 |
| 1.595~1.625 | 4 | 0.08 |
| 1.6254~1.655 | 6 | 0.12 |
| 1.655~1.685 | 11 | 0.22 |
| 1.685~1.715 | 17 | 0.34 |
| 1.715~1.745 | 6 | 0.12 |
| 1.745~1.775 | 4 | 0.08 |
| 合 计 | 50 | 1 |
分析 (1)根据频数、频率、总人数的定义即可解决问题;
(2)求出身高不低于1.655m且不高于1.715m的学生即可解决问题;
(3)利用样本估计总体的思想解决问题即可;
解答 解:(1)身高在1.685~1.715的频数为0.34×50=17(人),
∴身高在1.595~1.625的频数=50-2-6-11-17-6-4=4(人),频率为0.08,
1.715~1.745的频率为0.12.
故答案为4,0.08,17,0.12.
(2)估计这所学校17岁男生中,如果该校17岁男生共有350名,那么在这个身高范围内的人数估计有多少人所占的百分比为$\frac{11+17}{50}$=56%.
( 3)身高在1.685~1.715范围内的频数最多,如果该校17岁男生共有350名,那么在这个身高范围内的人数估计有350×0.34=119(人).
点评 本题考查频率分布表,解题的关键是熟练掌握基本概念,灵活应用所学知识解决问题.


科目:初中数学 来源: 题型:解答题
 如图,在直角三角形ABC中,∠ACB=90°,∠A=33°,将三角形ABC沿AB方向向右平移得到三角形DEF.
如图,在直角三角形ABC中,∠ACB=90°,∠A=33°,将三角形ABC沿AB方向向右平移得到三角形DEF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知:EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试说明AB∥MN.
如图,已知:EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试说明AB∥MN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
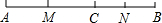 如图,点C在线段AB上,AC=12厘米,CB=8厘米,点M、N分别是AC、BC的中点.
如图,点C在线段AB上,AC=12厘米,CB=8厘米,点M、N分别是AC、BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D,过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE,对于下列结论:①AD=AE;②△CBA∽△CDE;③弧BD=$\frac{2}{3}$弧AD;④AE为⊙O的切线,结论一定正确的是( )
如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D,过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE,对于下列结论:①AD=AE;②△CBA∽△CDE;③弧BD=$\frac{2}{3}$弧AD;④AE为⊙O的切线,结论一定正确的是( )| A. | ②③ | B. | ②④ | C. | ①② | D. | ①③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com